Ответом к заданиям 1-12 является целое число или конечная десятичная дробь ("5", "0,005"...). Запишите ответ в поле ответа БЕЗ ПРОБЕЛОВ И ДРУГИХ ЛИШНИХ СИМВОЛОВ, а затем нажмите кнопку "ПРОВЕРИТЬ".
|
| |||
|
Тетрадь стоит 13 рублей. Сколько рублей заплатит покупатель за 40 тетрадей, если при покупке больше 30 тетрадей магазин делает скидку 10% от стоимости всей покупки? | |||
| |||
На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа в Томске впервые выпало ровно 0,5 миллиметра осадков.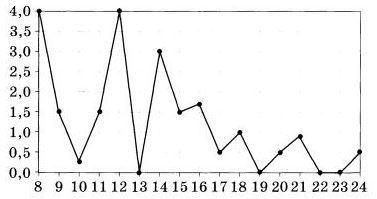 | |||
| |||
Найдите площадь трапеции, изображённой на рисунке.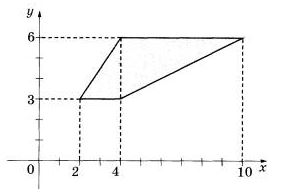 | |||
| |||
|
В фирме такси в наличии 60 легковых автомобилей; 27 из них чёрного цвета с жёлтыми надписями на боках, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями. | |||
| |||
Найдите корень уравнения 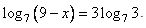 | |||
| |||
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Боковая сторона треугольника равна 12. Найдите площадь этого треугольника.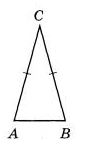 | |||
| |||
На рисунке изображён график функции у = f(x), определённой на интервале (-3;10). Найдите количество точек, в которых производная функции f(x) равна 0.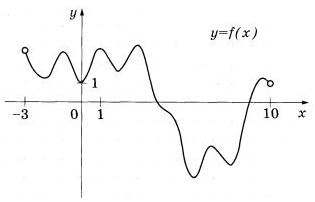 | |||
| |||
|
В цилиндрический сосуд налили 500 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,2 раза. Найдите объём детали. Ответ выразите в куб. см. | |||
| |||
Найдите значение выражения 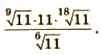 | |||
| |||
Водолазный колокол, содержащий v = 2,5 моля воздуха при давлении  = 1,25 атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления = 1,25 атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления  . Работа, совершаемая водой при сжатии воздуха, определяется выражением . Работа, совершаемая водой при сжатии воздуха, определяется выражением 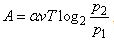 , где , где 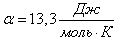 — постоянная, Т = 300 К — температура воздуха. Найдите, какое давление — постоянная, Т = 300 К — температура воздуха. Найдите, какое давление 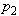 (в атм.) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 19 950 Дж. (в атм.) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 19 950 Дж. | |||
| |||
|
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 54 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды? | |||
| |||
Найдите точку максимума функции 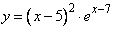 . . | |||
| |||
а) Решите уравнение 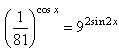 . .
б) Укажите корни этого уравнения, принадлежащие отрезку 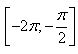 . . | |||
| |||
|
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами АВ=√11 и ВС = 2√3. Длины боковых рёбер пирамиды SA = 5, SB = 6, SD = √37.
а) Докажите, что SA — высота пирамиды. б) Найдите угол между прямой SC и плоскостью ASB. | |||
| |||
Решите неравенство 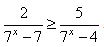 . . | |||
| |||
|
В прямоугольной трапеции ABCD с прямым углом при вершине А расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая — боковых сторон, меньшего основания ВС и первой окружности. а) Прямая, проходящая через центры окружностей, пересекает основание AD в точке Р. Докажите, что AP/PD = sinD. б) Найдите площадь трапеции, если радиусы окружностей равны  и и 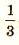 | |||
| |||
|
15 января планируется взять кредит в банке на сумму 1,8 млн рублей на 24 месяца. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; - со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; - 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Какую сумму нужно вернуть банку в течение первого года кредитования? | |||
| |||
Найти все значения параметра a, при каждом из которых множество значений функции 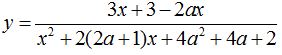 содержит отрезок [0;1]. содержит отрезок [0;1]. | |||
| |||
Каждый из группы учащихся сходил в кино или в театр, при этом возможно, что кто-то из них мог сходить и в кино, и в театр. Известно, что в театре мальчиков было не более 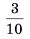 от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более 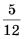 от общего числа учащихся группы, посетивших кино. от общего числа учащихся группы, посетивших кино. а) Могло ли быть в группе 8 мальчиков, если дополнительно известно, что всего в группе было 16 учащихся? б) Какое наибольшее количество мальчиков могло быть в группе, если дополнительно известно, что всего в группе было 16 учащихся? в) Какую наименьшую долю могли составлять девочки от общего числа учащихся в группе без дополнительного условия пунктов а) и б)? | |||
Результаты:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |