Упр.785 ГДЗ Атанасян 10-11 класс по геометрии (Геометрия)
Решение #1
Решение #2
Решение #3


Рассмотрим вариант решения задания из учебника Атанасян, Бутузов, Кадомцев 11 класс, Просвещение:
Докажите, что центры граней правильного додекаэдра являются вершинами правильного икосаэдра.
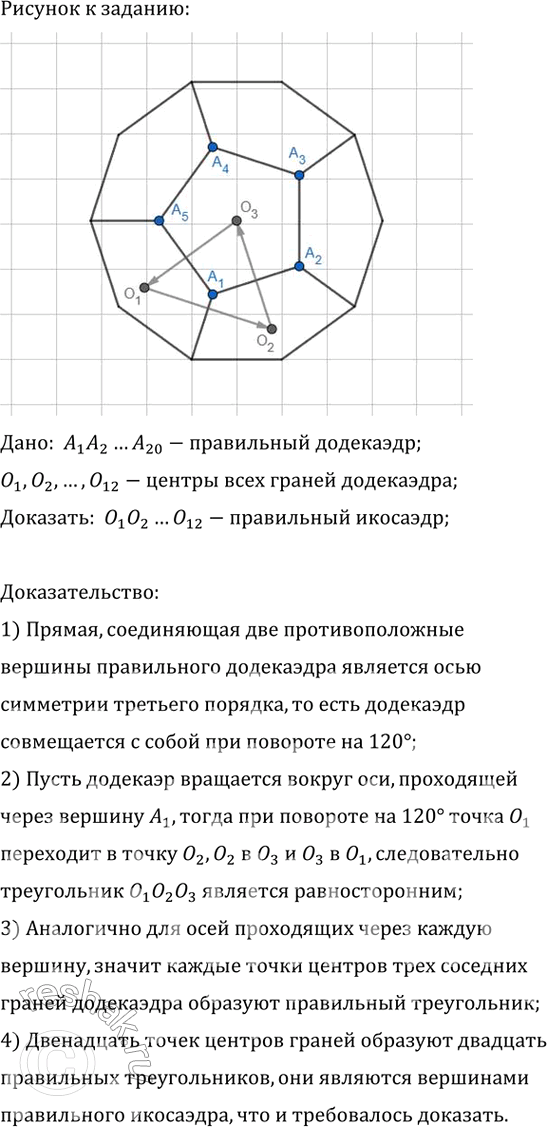
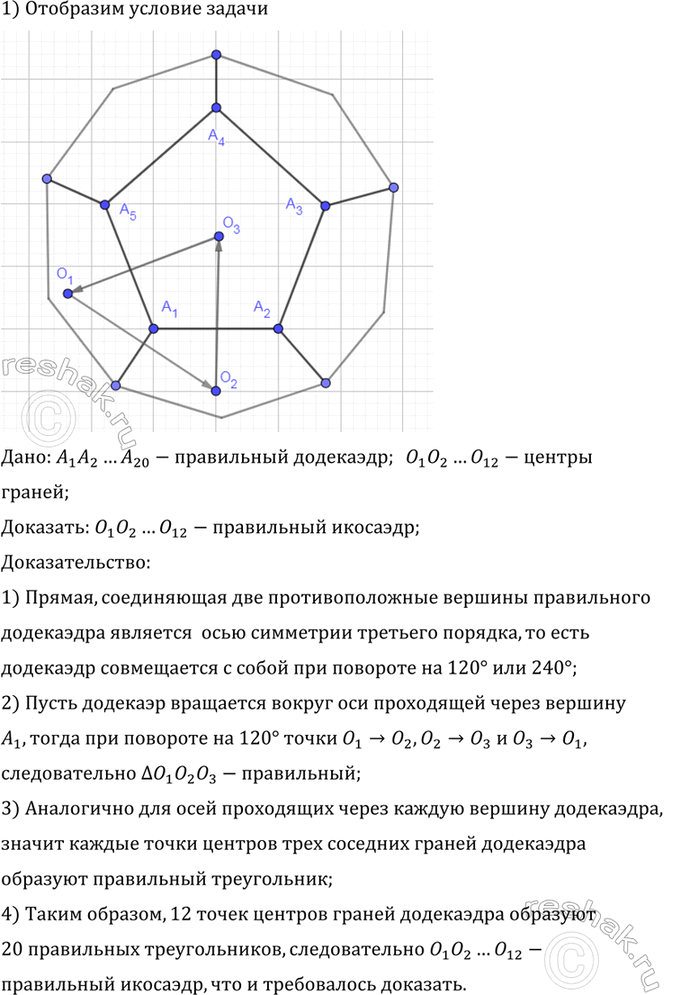
Дано: A_1 A_2…A_20-правильный додекаэдр; O_1,O_2,…,O_12-центры всех граней додекаэдра;
Доказать: O_1 O_2…O_12-правильный икосаэдр;
Доказательство:
1) Прямая,соединяющая две противоположные вершины правильного додекаэдра является осью
симметрии третьего порядка,то есть додекаэдр совмещается с собой при повороте на 120;
2) Пусть додекаэр вращается вокруг оси,проходящей через вершину A_1,тогда при повороте на 120 точка O_1 переходит в точку O_2,O_2 в O_3 и O_3 в O_1,следовательно треугольник O_1 O_2 O_3 является равносторонним;
3) Аналогично для осей проходящих через каждую вершину,значит каждые точки центров трех соседних граней додекаэдра образуют правильный треугольник;
4) Двенадцать точек центров граней образуют двадцать правильных треугольников,они являются вершинами правильного икосаэдра,что и требовалось доказать.
Популярные решебники 11 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением





