Стр.41 Часть 2 ГДЗ Дорофеев Миракова 4 класс (Математика)
Решение #1




Решение #2













Рассмотрим вариант решения задания из учебника Дорофеев, Миракова, Бука 4 класс, Просвещение:
3. От двух пристаней, расстояние между которыми 120 км, навстречу друг другу отправились моторная лодка и катер. Скорость моторной лодки 25 км/ч, а скорость катера 35 км/ч. Через сколько часов лодка и катер встретятся?
Составь и реши три задачи, обратные данной.
4. Вычисли значения выражений.
(1 250 - 1 125) · 3 + 125 · 100 20 450 - 20 405 + 2 145
1 250 + 7 500 : 5 + 2 530 38 000 + 95 · 200 - 3 700
(10 500 - 7 050) : 10 + 75 5 700 · (32 · 50 - 4 · 400)
5. Вычисли периметр и площадь прямоугольника, длина которого равна 7 м, а ширина в 10 раз меньше.
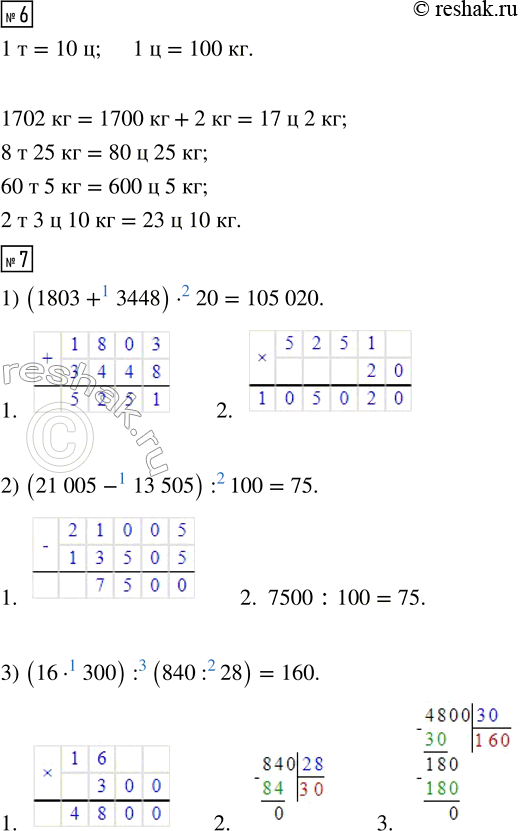
6. Вырази в центнерах и килограммах:
1 702 кг; 8 т 25 кг; 60 т 5 кг; 2 т 3 ц 10 кг.
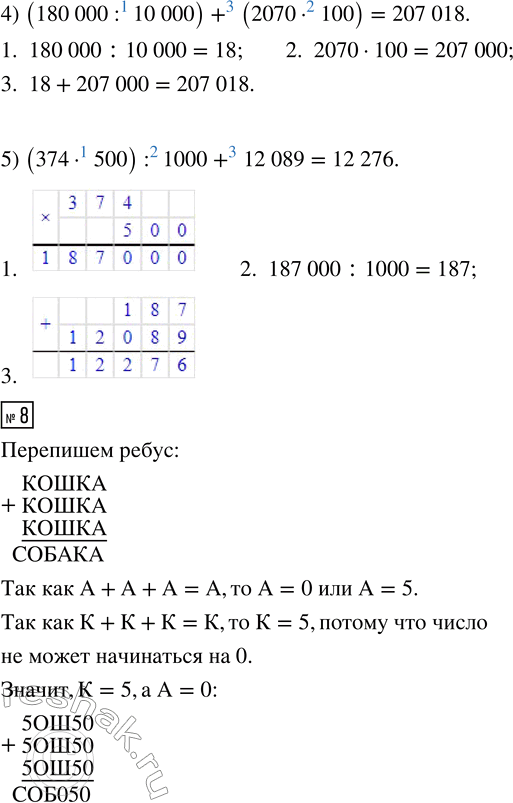
7. Запиши выражения и вычисли их значения.
1) Сумму чисел 1 803 и 3 448 увеличить в 20 раз.
2) Разность чисел 21 005 и 13 505 уменьшить в 100 раз.
3) Произведение чисел 16 и 300 разделить на частное от деления числа 840 на 28.
4) Частное чисел 180 000 и 10 000 увеличить на произведение чисел 2 070 и 100.
5) Число 374 умножить на 500, полученное произведение разделить на 1 000 и к частному прибавить 12 089.
8. Расшифруй ребус. (Одинаковыми буквами обозначены одинаковые цифры, разными — разные.) Попробуй найти два варианта ответа.
КОШКА + КОШКА + КОШКА = СОБАКА
3.
Для того, чтобы найти время, необходимо пройденный путь разделить на скорость: t=S:V
Скорость сближения – это величина, на которую уменьшится расстояние между двумя объектами за единицу времени.
Для того, чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, необходимо сложить их скорости: V_(сбл.)=V_1+V_2
Объекты отправились навстречу друг другу. Скорость моторной лодки 25 км/ч, а скорость катера 35 км/ч.
Для того, чтобы найти скорость их сближения, необходимо сложить скорости, с которыми они движутся.
V_(сбл.)=25+35=60 (км/ч) – скорость сближения лодки и катера.
Расстояние между пристанями 120 км. Скорость сближения моторной лодки и катера равна 60 км/ч.
Для того, чтобы найти время их встречи, необходимо разделить расстояние между ними на скорость их сближения.
t=S:V=120:60=2 (ч) – они встретятся.
Ответ: через 2 часа.
Нам уже знакомы задачи, условия и решения которых взаимосвязаны. Если одно из данных в условии задачи посчитать неизвестным, а вычисленное неизвестное взять за данное, то получится задача, обратная данной.
Запишем условие и схему для первой обратной задачи.
От двух пристаней, расстояние между которыми 120 км, навстречу дуг другу отправились моторная лодка и катер. Через 2 часа они встретились. Скорость моторной лодки 25 км/ч. Найди скорость катера.
Для того, чтобы найти скорость, необходимо расстояние разделить на время, V=S:t.
Расстояние между пристанями равно 120 км, а время, через которое встретились моторная лодка и катер – 2 часа. Разделив расстояние между лодкой и катером на время, через которое они встретятся, мы найдём скорость их сближения.
120:2=60 (км/ч) – скорость сближения лодки и катера.
Скорость сближения моторной лодки и катера 60 км/ч, а скорость моторной лодки – 25 км/ч. Для того, чтобы найти скорость катера, необходимо вычесть из скорости сближения скорость моторной лодки.
60-25=35 (км/ч) – скорость катера.
Ответ: 35 км/ч.
Запишем условие и схему для второй обратной задачи.
От двух пристаней, расстояние между которыми 120 км, навстречу друг другу отправились моторная лодка и катер. Через 2 часа они встретились. Скорость катера 35 км/ч. Найди скорость моторной лодки.
Для того, чтобы найти скорость, необходимо расстояние разделить на время, V=S:t.
Расстояние между пристанями равно 120 км, а время, через которое встретились моторная лодка и катер – 2 часа. Разделив расстояние между лодкой и катером на время, через которое они встретятся, мы найдём скорость их сближения.
120:2=60 (км/ч) – скорость сближения лодки и катера.
Скорость сближения моторной лодки и катера 60 км/ч, а скорость катера – 35 км/ч. Для того, чтобы найти скорость моторной лодки, необходимо вычесть из скорости сближения скорость катера.
60-35=25 (км/ч) – скорость моторной лодки.
Ответ: 25 км/ч.
Запишем условие и схему для третьей обратной задачи.
От двух пристаней, навстречу друг другу отправились моторная лодка и катер. Через 2 часа они встретились. Скорость моторной лодки 25 км/ч, а скорость катера 35 км/ч. Найди расстояние между двумя пристанями.
Необходимо найти скорость сближения моторной лодки и катера. Объекты отправились навстречу друг другу. Скорость моторной лодки 25 км/ч, а скорость катера 35 км/ч. Для того, чтобы найти скорость их сближения, необходимо сложить скорости, с которыми они движутся.
35+25=60 (км/ч)-скорость сближения лодки и катера.
Расстояние равно скорости, умноженной на время движения.
S=V•t, где V - скорость движения объекта, t – время и S – расстояние, пройденное за это время.
S=V•t=60•2=120 (км) – расстояние между пристанями.
Ответ: 120 км.
4.
Действия в числовых выражениях выполняются в следующем порядке:
1. действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Для того, чтобы умножить целое число на 10, 100, 1 000 и так далее, необходимо приписать справа к этому числу столько нулей, сколько их в числах 10, 100, 1 000.
1 2 4 3
(1 250-1 125)•3+125•100=125•3+125•100=
=375+125•100=375+12 500=12 875
1 250
1 125
125
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, тысячи под тысячами): 1 250-1 125.
Вычитаем единицы: из 0 единиц нельзя вычесть 5 единиц, поэтому возьмём из 5 десятков 1 десяток, то есть 10 единиц (для того, чтобы не забыть, ставим точку над цифрой 5). 10+0=10.
Вычтем: 10-5=5. Пишем 5 под единицами.
Вычитаем десятки: было 5 десятков, но после того, как заняли 1 десяток при вычитании единиц, осталось 4 десятка.
Вычтем: 4-2=2. Пишем 2 под десятками.
Вычитаем сотни: 2-1=1. Пишем 1 под сотнями.
Вычитаем тысячи: 1-1=0. 0 под высшим разрядом не пишут.
Читаем ответ: 125.
125
3
375
Пишу: 125•3.
Умножаю единицы: 5•3=15. 15 ед. – это 1 дес. 5 единиц; пишу 5 под единицами, а 1 десяток запомню и прибавлю к десяткам.
Умножаю десятки: 2•3=6, да ещё 1.
6+1=7. Пишу 7 под десятками.
Умножаю сотни: 1•3=3. Пишу 3 под сотнями.
Читаю ответ: 375.
2 1 3
1 250+7 500:5+2 530=1 250+1 500+2 530=
=2 750+2 530=5 280
7500 5
5 1500
25
25
0
Пишем: 7 500:5.
Первое неполное делимое – 7 тысяч. Значит, в частном будет 4 цифры.
Делю тысячи: разделю 7 на 5, получу 1 – столько тысяч будет в частном.
Умножу 5 на 1, получу 5 – столько тысяч разделили.
Вычту: 7-5=2 - столько тысяч осталось разделить.
Делю сотни: 2 тысячи 5 сотен – это 25 сотен.
Разделю 25 на 5, получу 5 - столько сотен будет в частном.
Умножу 5 на 5, получу 25 - столько сотен разделили.
Вычту: 25-25=0 – сотни разделили все.
Десятков и сотен осталось по 0, поэтому в частном на месте десятков и сотен пишем нули, так как при делении 0 на любое число, получится 0.
Читаю ответ: 1 500.
2 750
2 530
5 280
Складываем единицы: 0+0=0. Пишу 0 под единицами.
Складываю десятки: 5+3=8. Пишу 8 под десятками.
Складываю сотни: 7+5=12. 12 сотен – это 1 тысяча 2 сотни; пишу 2 под сотнями, а 1 тысячу запомню и прибавлю к тысячам.
Складываю тысячи: 2+2=4, да ещё 1.
4+1=5. Пишу 5 под тысячами.
Читаю ответ: 5 280.
1 2 3
(10 500-7 050) :10+75=3 450:10+75=345+75=420
10 500
7 050
3 450
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч):
10 500-7 050.
Вычитаем единицы: 0-0=0. Пишем 0 под единицами.
Вычитаем десятки: из 0 дес. нельзя вычесть 5 дес., поэтому возьмём из 5 сот. 1 сот., то есть 10 дес. (для того, чтобы не забыть, ставим точку над цифрой 5). 10+0=10.
Вычтем: 10-5=5. Пишем 5 под десятками.
Вычитаем сотни: было 5 сотен, но после того, как заняли 1 сотню при вычитании десятков, осталось 4 сотни.
Вычтем: 4-0=4. Пишем 4 под сотнями.
Вычитаем единицы тысяч: из 0 ед. тыс. нельзя вычесть 7 ед. тыс., поэтому займём из 1 дес. тыс. 1 дес. тыс., то есть 10 ед. тыс. (для того, чтобы не забыть, ставим точку над цифрой 1). 10+0=10.
Вычтем: 10-7=3. Пишем 3 под единицами тысяч.
Вычитаем десятки тысяч: был 1 десяток тысяч, но 1 десяток тысяч заняли при вычитании единиц тысяч, осталось 0 десятков тысяч. 0 под высшим разрядом принято не писать.
Читаем ответ: 3 450.
345
75
420
Складываем единицы: 5+5=10. 10 ед. – это 1 дес. 0 ед.; пишу 0 под единицами, а 1 десяток запомню и прибавлю к десяткам.
Складываю десятки: 4+7=11, да ещё 1.
11+1=12. 12 десятков – это 1 сотня 2 десятка; пишу 2 под десятками, а 1 сотню запомню и прибавлю к сотням.
Складываю сотни: 3 сотни, да ещё 1.
3+1=4. Пишу 4 под сотнями.
Читаю ответ: 420.
1 2
20 450-20 405+2 145=45+2 145=2 190
2 1 3
38 000+95•200-3 700=38 000+19 000-3 700=
=57 000-3 700=53 300
57 000
3 700
53 300
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч):
57 000-3 700.
Вычитаем единицы: 0-0=0. Пишем 0 под единицами.
Вычитаем десятки: 0-0=0. Пишем 0 под десятками.
Вычитаем сотни: из 0 сотен нельзя вычесть 7 сотен, поэтому возьмём из 7 единиц тысяч 1 единицу тысяч, то есть 10 сотен (для того, чтобы не забыть, ставим точку над цифрой 7). 10+0=10.
Вычтем: 10-7=3. Пишем 3 под сотнями.
Вычитаем единицы тысяч: было 7 ед. тыс., но после того, как заняли 1 ед. тыс. при вычитании сотен, осталось 6 единиц тысяч.
Вычтем: 6-3=3. Пишем 3 под единицами тысяч.
Спускаем в ответ 5 десятков тысяч.
Читаем ответ: 53 300.
4 1 3 2
5 700•(32•50-4•400)=5 700•(1 600-4•400)=
=5 700•(1 600-1 600)=5 700•0=0
5.
Периметр прямоугольника – это сумма длин всех его сторон.
Периметр прямоугольника можно найти двумя способами:
- сложить все стороны;
- сложить длину и ширину и удвоить их сумму.
Для того, чтобы найти площадь прямоугольника, необходимо умножить его длину на ширину.
S=a•b, где S - площадь, a и b - смежные стороны.
Переведём метры в сантиметры. Известно, что 1 м=100 см, тогда 7 м=7•1 м=7•100 см=700 см.
Для того, чтобы узнать, во сколько раз одно число больше или меньше другого, необходимо большее число разделить на меньшее.
Найдём ширину прямоугольника.
700:10=70 (см) – ширина прямоугольника.
Найдём периметр прямоугольника.
P=(700+70)•2=770•2=1 540 (см).
Переведём сантиметры в метры.
1 540 см=1 500 см+40 см=15•100 см+40 см=
=15•1 м+40 см=15 м+40 см=15 м 40 см.
Найдём площадь прямоугольника.
S=700•70=49 000 (см^2).
Вспомним перевод мер площади: 1 дм^2=100 см^2.
Переведём квадратные сантиметры в квадратные дециметры.
49 000 см^2=490•100 см^2=490•1 дм^2=490 дм^2.
Ответ: 15 м 40 см; 490 дм^2.
7.
1) Для того, чтобы увеличить число в n раз, можно его умножить на n.
Сумма в математике записывается с помощью знака «плюс».
Для того, чтобы умножить число на круглые десятки, необходимо умножить его на число десятков и к полученному произведению приписать 0.
Запишем выражение:
(1 803+3 448)•20=5 251•20=105 020
1 803
3 448
5 251
Складываем единицы: 3+8=11. 11 ед. – это 1 дес. 1 ед.; пишу 1 под единицами, а 1 десяток запомню и прибавлю к десяткам.
Складываю десятки: 0+4=4, да ещё 1.
4+1=5. Пишу 5 под десятками.
Складываю сотни: 8+4=12. 12 сотен – это 1 тысяча 2 сотни; пишу 2 под сотнями, а 1 тысячу запомню и прибавлю к тысячам.
Складываю тысячи: 1+3=4, да ещё 1.
4+1=5. Пишу 5 под тысячами.
Читаю ответ: 5 251.
2) Для того, чтобы уменьшить число в n раз, можно его разделить на n.
Разность в математике записывается с помощью знака «минус».
Запишем выражение:
(21 005-13 505) :100=7 500:100=75
21 005
13 505
7 500
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч): 21 005-13 505.
Вычитаем единицы: 5-5=0. Пишем 0 под единицами.
Вычитаем десятки: 0-0=0. Пишем 0 под десятками.
Вычитаем сотни: из 0 сот. нельзя вычесть 5 сот., поэтому возьмём из 1 единицы тысяч 1 единицу тысяч, то есть 10 сотен (для того, чтобы не забыть, ставим точку над цифрой 1). 10+0=10.
Вычтем: 10-5=5. Пишем 5 под сотнями.
Вычитаем единицы тысяч: была 1 ед. тыс., но после того, как заняли 1 ед. тыс. при вычитании сотен, осталось 0 единиц тысяч. Из 0 единиц тысяч нельзя вычесть 3 единицы тысяч, поэтому возьмём из 2 десятков тысяч 1 дес. тысяч, то есть 10 ед. тыс. (для того, чтобы не забыть, ставим точку над цифрой 2). 10+0=10.
Вычтем: 10-3=7. Пишем 7 под единицами тысяч.
Вычитаем десятки тысяч: было 2 дес. тыс., но 1 дес. тыс. заняли при вычитании ед. тыс., остался 1 дес. тыс.
Вычтем: 1-1=0. 0 под высшим разрядом принято не писать.
Читаем ответ: 7 500.
3) Произведение в математике записывается с помощью знака «умножить».
Частное в математике записывается с помощью знака «разделить».
Запишем выражение:
(16•300) :(840:28)=4 800:(840:28)=4 800:30=
=480:3=160
4) Запишем выражение:
180 000:10 000+2 070•100=18:1+2 070•100=
=18+2 070•100=18+207 000=207 018
5) Запишем уравнение:
374•500:1 000+12 089=187 000:1 000+12 089=
=187+12 089=12 276
374
5
1 870
Пишу: 374•5.
Умножаю единицы: 4•5=20. 20 ед. – это 2 дес. 0 единиц; пишу 0 под единицами, а 2 десятка запомню и прибавлю к десяткам.
Умножаю десятки: 7•5=35, да ещё 2.
35+2=37. 37 десятков – это 3 сотни 7 десятков; пишу 7 под десятками, а 3 сотни запомню и прибавлю к сотням.
Умножаю сотни: 3•5=15, да ещё 3.
15+3=18. 18 сот. – это 1 тыс. 8 сот.; пишу 8 под сот., а 1 тыс. пишу под тысячами, так как других тысяч для умножения нет.
Допишу к произведению справа два нуля.
Читаю ответ: 187 000.
Похожие решебники
Популярные решебники 4 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением






