Стр.49 Часть 2 ГДЗ Дорофеев Миракова 4 класс (Математика)
Решение #1

Решение #2




Рассмотрим вариант решения задания из учебника Дорофеев, Миракова, Бука 4 класс, Просвещение:
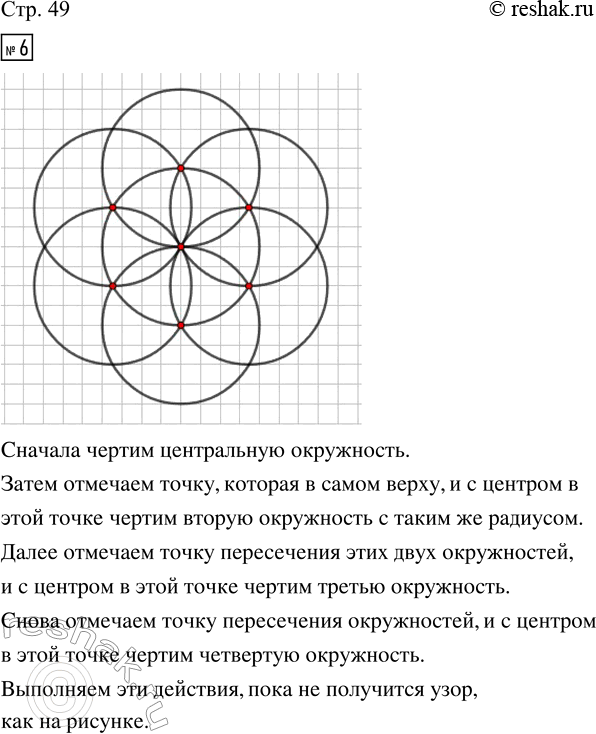
6. Начерти в тетради такой узор, как на рисунке. Начни с вычерчивания центральной окружности. Отметь на ней любую точку и проведи, не меняя радиуса, окружность с центром в этой точке. Догадайся, как надо действовать дальше.
Начертим центральную окружность с помощью циркуля.
Подберём удобный радиус окружности, например 2 см – такое расстояние должно быть между карандашом и иглой циркуля.
Ставим иглу в точку, где хотим, чтобы был центр окружности.
Рисуем окружность, поворачивая карандаш вокруг иглы.
Отметим точку на окружности.
В отмеченной точке будет центр новой окружности.
Нарисуем окружность с центром в новой точке.
Не изменяем радиус окружности. Он остаётся 2 см.
Ставим иглу в отмеченную точку. Рисуем окружность.
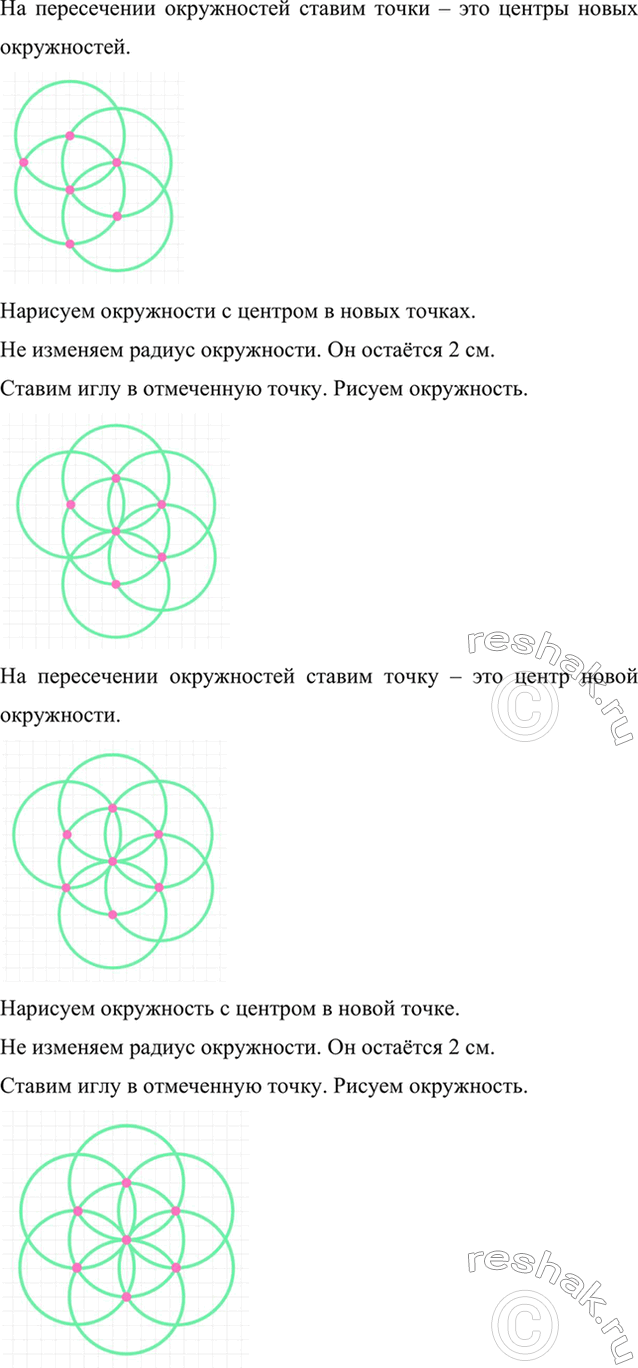
На пересечении окружностей ставим точки – это центры новых окружностей.
Нарисуем окружности с центром в новых точках.
Не изменяем радиус окружности. Он остаётся 2 см.
Ставим иглу в отмеченную точку. Рисуем окружность.
На пересечении окружностей ставим точки – это центры новых окружностей.
Нарисуем окружности с центром в новых точках.
Не изменяем радиус окружности. Он остаётся 2 см.
Ставим иглу в отмеченную точку. Рисуем окружность.
На пересечении окружностей ставим точку – это центр новой окружности.
Нарисуем окружность с центром в новой точке.
Не изменяем радиус окружности. Он остаётся 2 см.
Ставим иглу в отмеченную точку. Рисуем окружность.
7. Сравни.
12 км 900 м - 8 км 560 м и 2 км 320 м + 1 км 700 м
65 кг 020 г + 10 кг 870 г и 100 кг - 24 кг 300 г
12 км 900 м-8 км 560 м 2 км 320 м+1 км 700 м
Вспомним, что 1 км=1 000 м.
Решим выражение в левой части неравенства.
12 км 900 м-8 км 560 м=
=(12 км+900 м)-(8 км+560 м)=
=(12•1 км+900 м)-(8•1 км+560 м)=
=(12•1 000 м+900 м)-(8•1 000 м+560 м)=
=(12 000 м+900 м)-(8 000 м+560 м)=
=12 900 м-8 560 м=4 340 м.
12 900
8 560
4 340
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, тысячи под тысячами): 12 900-8 560.
Вычитаем единицы: 0-0=0. Пишу 0 под единицами.
Вычитаем десятки: из 0 десятков нельзя вычесть 6 десятков, поэтому возьмём из 9 сотен 1 сотню, то есть 10 десятков (для того, чтобы не забыть, ставим точку над цифрой 9). 10+0=10.
Вычтем: 10-6=4. Пишем 4 под десятками.
Вычитаем сотни: было 9 сотен, но после того, как заняли 1 сотню при вычитании десятков, осталось 8 сотен.
Вычтем: 8-5=3. Пишем 3 под сотнями.
Вычитаем единицы тысяч: из 2 ед. тыс. нельзя вычесть 8 ед. тыс., поэтому возьмём из 1 дес. тыс. 1 дес. тыс., то есть 10 ед. тыс. (для того, чтобы не забыть, ставим точку над цифрой 1). 10+2=12.
Вычтем: 12-8=4. Пишем 4 под единицами тысяч.
Вычитаем десятки тысяч: был 1 десяток тысяч, но после того, как заняли 1 десяток тысяч при вычитании единиц тысяч, осталось 0 десятков тысяч. 0 под высшим разрядом принято не писать.
Читаем ответ: 4 340.
Решим выражение в правой части неравенства.
2 км 320 м+1 км 700 м=(2 км+320 м)+(1 км+700 м)=
=(2•1 км+320 м)+(1 км+700 м)=
=(2•1 000 м+320 м)+(1 000 м+700 м)=
=(2 000 м+320 м)+(1 000 м+700 м)=2 320 м+1 700 м==4 020 м.
Так как 4 340 м > 4 020 м, значит и
12 км 900 м-8 км 560 м > 2 км 320 м+1 км 700 м.
65 кг 020 г+10 кг 870 г 100 кг-24 кг 300 г
Вспомним о том, что 1 кг=1 000 кг.
Решим выражение в левой части неравенства.
65 кг 020 г+10 кг 870 г=(65 кг+020 г)+(10 кг+870 г)==(65•1 кг+20 г)+(10•1 кг+870 г)=
=(65•1 000 г+20 г)+(10•1 000 г+870 г)=
=(65 000 г+20 г)+(10 000 г+870 г)=
=65 020 г+10 870 г=75 890 г.
Решим выражение в правой части неравенства.
100 кг-24 кг 300 г=100 кг-(24 кг+300 г)=
=100•1 кг-(24•1 кг+300 г)=
=100•1 000 г-(24•1 000 г+300 г)=
=100 000 г-(24 000 г+300 г)=100 000 г-24 300 г=
=75 700 г.
100 000
24 300
75 700
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч): 100 000-24 300.
Вычитаем единицы: 0-0=0. Пишу 0 под единицами.
Вычитаем десятки: 0-0=0. Пишу 0 под десятками.
Вычитаем сотни: из 0 сот. нельзя вычесть 3 сот., из 0 ед. тыс. занять нельзя, из 0 дес. тыс. занять нельзя, поэтому возьмём из 1 сот. тыс. 1 сот. тыс., то есть 10 дес. тыс. (для того, чтобы не забыть, ставим точку над цифрой 1). Распределим 10 дес. тысяч, как 9 десятков тысяч, 9 единиц тысяч 10 сотен. 10+0=10.
Вычтем: 10-3=7. Пишем 7 под сотнями.
Вычитаем единицы тысяч: было 0 ед. тыс., но после того, как заняли 1 сот. тыс. при вычитании сотен, осталось 9 единиц тысяч.
Вычтем: 9-4=5. Пишем 5 под единицами тысяч.
Вычитаем десятки тысяч: было 0 дес. тыс., но после того, как заняли 1 сот. тыс. при вычитании сот., осталось 9 десятков тысяч.
Вычтем: 9-2=7. Пишем 7 под десятками тысяч.
Вычитаем сотни тысяч: была 1 сот. тыс., но после того, как заняли 1 сот. тысяч при вычитании сотен, осталось 0 сотен тысяч.
0 под высшим разрядом принято не писать.
Читаем ответ: 75 700.
Так как 75 890 г > 75 700 г, значит и
65 кг 020 г+10 кг 870 г > 100 кг-24 кг 300 г.
8. В день рождения Маши её младший брат решил пошутить. Он положил в три одинаковые коробки конфеты, печенье и торт. На коробках были этикетки: КОНФЕТЫ, ПЕЧЕНЬЕ, ТОРТ. Ни одна надпись не соответствовала тому продукту, который лежал в коробке. Брат сказал Маше, что конфеты не лежат в коробке с этикеткой ТОРТ. В какой же коробке находился торт?
Похожие решебники
Популярные решебники 4 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением






