Стр.58 Часть 2 ГДЗ Дорофеев Миракова 4 класс (Математика)
Решение #1


Решение #2







Рассмотрим вариант решения задания из учебника Дорофеев, Миракова, Бука 4 класс, Просвещение:
1. Из пунктов А и В, расстояние между которыми равно 100 км, одновременно в одном направлении выехали грузовик и гужевая повозка. Скорость грузовика 40 км/ч, а скорость гужевой повозки 20 км/ч. На сколько километров сократится расстояние между ними через 1 ч? через 2 ч? Через сколько часов грузовик сможет догнать гужевую повозку?
2. Составь по рисунку задачу, аналогичную задаче 1.
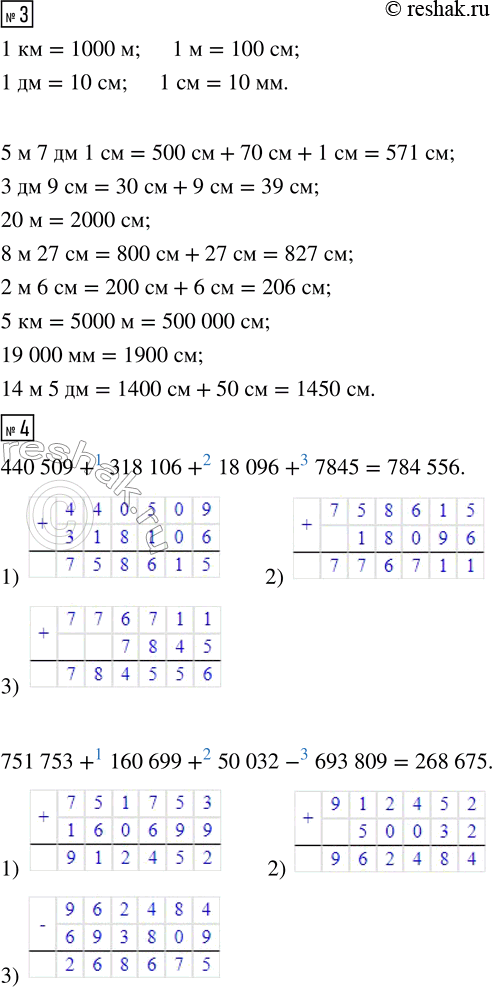
3. Вырази в сантиметрах:
5 м 7 дм 1 см; 3 дм 9 см; 20 м; 8 м 27 см; 2 м 6 см; 5 км; 19 000 мм; 14 м 5 дм.
4. Выполни действия. Сделай проверку с помощью калькулятора.
440 509 + 318 106 + 18 096 + 7 845
751 753 + 160 699 + 50 032 - 693 809
Для того, чтобы умножить число на 10, 100, 1 000, 10 000 или 100 000, необходимо приписать к этому числу справа соответственно один, два, три, четыре или пять нулей.
Вспомним, сколько сантиметров в 1 дециметре и 1 метре:
1 дм=10 см,1 м=100 см.
5 м 7 дм 1 см=5 м+7 дм+1 см=5•1 м+7•1 дм+1 см=
=5•100 см+7•10 см+1 см=500 см+70 см+1 см=
=570 см+1 см=571 см.
3 дм 9 см=3 дм+9 см=3•1 дм+9 см=3•10 см+9 см=
=30 см+9 см=39 см.
20 м=20•1 м=20•100 см=2 000 см.
8 м 27 см=8 м+27 см=8•1 м+27 см=8•100 см+27 см==800 см+27 см=827 см.
2 м 6 см=2 м+6 см=2•1 м+6 см=2•100 см+6 см=
=200 см+6 см=206 см.
Найдём, сколько сантиметров в 1 километре.
1 км=1 000 м и 1 м=100 см.
Значит, 1 км=1 000•100 см=100 000 см.
Тогда, 5 км=5•1 км=5•100 000 см=500 000 см.
Вспомним, сколько в 1 сантиметре миллиметров: 1 см=10 мм.
Для того, чтобы разделить число на 10, 100 или 1 000, необходимо отбросить у этого числа справа соответственно один, два или три нуля.
19 000 мм=19 000:10 см=1 900 см.
14 м 5 дм=14 м+5 дм=14•1 м+5•1 дм=
=14•100 см+5•10 см=1 400 см+50 см=1 450 см.
440 509+318 106+18 096+7 845=784 556
440 509
318 106
18 096
7 845
784 556
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч, сотни тысяч под сотнями тысяч):
440 509+318 106+18 096+7 845.
Складываем единицы: 9+6+6+5=15+11=26. 26 ед. – это 2 дес. 6 ед.; пишу 6 под ед., а 2 дес. запомню и прибавлю к дес.
Складываю десятки: 0+0+9+4=0+13=13, да ещё 2.
13+2=15. 15 десятков - это 1 сотня 5 десятков; пишу 5 под десятками, а 1 сотню запомню и прибавлю к сотням.
Складываю сотни: 5+1+0+8=6+8=14, да ещё 1.
14+1=15. 15 сот. – это 1 ед. тыс. 5 сотен; пишу 5 под сотнями, а 1 единицу тысяч запомню и прибавлю к единицам тысяч.
Складываю единицы тысяч: 0+8+8+7=23, да ещё 1.
23+1=24. 24 ед. тыс. – это 2 дес. тыс. 4 ед. тыс.; пишу 4 под ед. тыс., а 2 дес. тысяч запомню и прибавлю к десяткам тысяч.
Складываю десятки тысяч: 4+1+1=5+1=6, да ещё 2.
6+2=8. Пишу 8 под десятками тысяч.
Складываю сотни тысяч: 4+3=7. Пишу 7 под сотнями тысяч.
Читаю ответ: 784 556.
751 753+160 699+50 032-693 809=962 484-693 809==268 675
751 753
160 699
50 032
962 484
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч, сотни тысяч под сотнями тысяч):
751 753+160 699+50 032.
Складываем единицы: 3+9+2=12+2=14. 14 ед. – это 1 дес. 4 ед.; пишу 4 под ед., а 1 дес. запомню и прибавлю к дес.
Складываю десятки: 5+9+3=14+3=17, да ещё 1.
17+1=18. 18 десятков - это 1 сотня 8 десятков; пишу 8 под десятками, а 1 сотню запомню и прибавлю к сотням.
Складываю сотни: 7+6+0=13+0=13, да ещё 1.
13+1=14. 14 сот. – это 1 ед. тыс. 4 сотни; пишу 4 под сотнями, а 1 единицу тысяч запомню и прибавлю к единицам тысяч.
Складываю единицы тысяч: 1+0+0=1+0=1, да ещё 1.
1+1=2. Пишу 2 под единицами тысяч.
Складываю десятки тысяч: 5+6+5=11+5=16. 16 дес. тыс. – это 1 сотня тысяч 6 десятков тысяч; пишу 6 под десятками тысяч, а 1 сотню тысяч запомню и прибавлю к сотням тысяч.
Складываю сотни тысяч: 7+1=8, да ещё 1.
8+1=9. Пишу 9 под сотнями тысяч.
Читаю ответ: 962 484.
962 484
693 809
268 675
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч, сотни тысяч под сотнями тысяч):
962 484-693 809.
Вычитаем единицы: из 4 единиц нельзя вычесть 9 единиц, поэтому возьмём из 8 десятков 1 десяток, то есть 10 единиц (для того, чтобы не забыть, ставим точку над цифрой 8). 10+4=14.
Вычтем: 14-9=5. Пишем 5 под единицами.
Вычитаем десятки: было 8 десятков, но после того, как заняли 1 десяток при вычитании единиц, осталось 7 десятков.
7-0=7. Пишем 7 под десятками.
Вычитаем сотни: из 4 сотен нельзя вычесть 8 сотен, поэтому возьмём из 2 единиц тысяч 1 единицу тысяч, то есть 10 сотен (для того, чтобы не забыть, ставим точку над цифрой 2). 10+4=14.
Вычтем: 14-8=6. Пишем 6 под сотнями.
Вычитаем единицы тысяч: было 2 ед. тыс., но после того, как заняли 1 ед. тыс. при вычитании сот., осталась 1 ед. тыс. Из 1 ед. тысяч нельзя вычесть 3 единиц тысяч, поэтому возьмём из 6 десятков тысяч 1 десяток тысяч, то есть 10 единиц тысяч (для того, чтобы не забыть, ставим точку над цифрой 6). 10+1=11.
Вычтем: 11-3=8. Пишем 8 под единицами тысяч.
Вычитаем десятки тысяч: было 6 дес. тыс., но после того, как заняли 1 дес. тыс. при вычитании ед. тыс., осталось 5 дес. тыс. Из 5 дес. тысяч нельзя вычесть 9 десятков тысяч, поэтому займём из 9 сотен тысяч 1 сотню тысяч, то есть 10 десятков тысяч (для того, чтобы не забыть, ставим точку над цифрой 9). 10+5=15.
Вычтем: 15-9=6. Пишем 6 под десятками тысяч.
Вычитаем сотни тысяч: было 9 сот. тыс., но после того, как заняли 1 сот. тыс. при вычитании дес. тыс., осталось 8 сот. тысяч.
Вычтем: 8-6=2. Пишем 2 под сотнями тысяч.
Читаем ответ: 268 675.
5. Надо заасфальтировать участок шоссе, длина которого 45 км 600 м. С одного конца участка заасфальтировали 7 км 590 м, а с другого — в 2 раза больше. Какое расстояние осталось заасфальтировать?
Запишем краткое условие задачи.
Участок шоссе - 45 км 600 м
Заасфальтировали с одного конца - 7 км 590 м
С другого конца - в 2 раза больше
Осталось - ? км ? м
Вспомним, сколько в 1 километре метров: 1 км=1 000 м.
Для того, чтобы умножить число на 10, 100, 1 000 или 10 000, необходимо приписать к этому числу справа соответственно один, два, три или четыре нуля.
Переведём 7 км 590 м в метры.
7 км 590 м=7 км+590 м=7•1 км+590 м=
=7•1 000 м+590 м=7 000 м+590 м=7 590 м.
Для того, чтобы найти, какое расстояние заасфальтировали с другого конца участка шоссе, необходимо расстояние, которое заасфальтировали с одного конца участка 7 590 м умножить на 2.
7 590
2
15 180
Пишу: 7 590•2.
Умножаю единицы: 0•2=0. Пишу 0 под единицами.
Умножаю десятки: 9•2=18. 18 дес. – это 1 сотня 8 десятков; пишу 8 под десятками, а 1 сотню запомню и прибавлю к сотням.
Умножаю сотни: 5•2=10, да ещё 1.
10+1=11. 11 сотен – это 1 единица тысяч 1 сотня; пишу 1 под сотнями, а 1 единицу тысяч запомню и прибавлю к ед. тысяч.
Умножаю единицы тысяч: 7•2=14, да ещё 1.
14+1=15. 15 ед. тыс. – это 1 дес. тысяч 5 единиц тысяч; пишу 5 под единицами тысяч, а 1 десяток тысяч пишу под десятками тысяч, так как других десятков тысяч для умножения нет.
Читаю ответ: 15 180.
Значит, 15 180 м дороги заасфальтировали с другого конца.
Для того, чтобы найти, какое расстояние заасфальтировали с обоих концов участка шоссе, необходимо к 7 590 м, заасфальтированных с одного конца, прибавить 15 180 м, заасфальтированных с другого конца.
7 590+15 180=22 770 (м) – заасфальтировали с обоих концов участка шоссе.
Переведём 45 км 600 м в метры.
45 км 600 м=45 км+600 м=45•1 км+600 м=
=45•1 000 м+600 м=45 000 м+600 м=45 600 м.
Для того, чтобы найти, какое расстояние осталось заасфальтировать, необходимо из длины участка шоссе 45 600 м вычесть расстояние, которое заасфальтировали, 22 770 м.
45 600
22 770
22 830
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч): 45 600-22 770.
Вычитаем единицы: 0-0=0. Пишем 0 под единицами.
Вычитаем десятки: из 0 десятков нельзя вычесть 7 десятков, поэтому возьмём из 6 сотен 1 сотню, то есть 10 десятков (для того, чтобы не забыть, ставим точку над цифрой 6). 10+0=10.
Вычтем: 10-7=3. Пишем 3 под десятками.
Вычитаем сотни: было 6 сот., но после того, как 1 сот. заняли при вычитании дес., осталось 5 сот. Из 5 сот. нельзя вычесть 7 сот., поэтому возьмём из 5 ед. тыс. 1 ед. тысяч, то есть 10 сотен (для того, чтобы не забыть, ставим точку над цифрой 5). 10+5=15.
Вычтем: 15-7=8. Пишем 8 под сотнями.
Вычитаем единицы тысяч: было 5 ед. тыс., но после того, как заняли 1 ед. тыс. при вычитании сот., осталось 4 единицы тысяч.
Вычтем: 4-2=2. Пишем 2 под единицами тысяч.
Вычитаем десятки тысяч: 4-2=2. Пишем 2 под дес. тысяч.
Читаем ответ: 22 830.
Значит, 22 830 м осталось заасфальтировать.
Переведём 22 830 м в километры.
22 830 м=22 000 м+830 м=22•1 000 м+830 м=
=22•1 км+830 м=22 км+830 м=22 км 830 м.
Ответ: 22 км 830 м.
6. Самый длинный день в году — 22 июня. В этот день солнце восходит в Москве в 3 ч 15 мин, а заходит в 20 ч 49 мин. Сколько времени продолжается в Москве самый длинный день?
Запишем краткое условие задачи.
Восход - 3 ч 15 мин
Закат - 20 ч 49 мин
День - ? ч ? мин
Для того, чтобы найти, сколько времени продолжается в Москве самый длинный день, необходимо из времени, когда солнце заходит, 20 ч 49 мин, вычесть время, когда солнце всходит, 3 ч 15 мин.
20 ч 49 мин-3 ч 15 мин=(20 ч+49 мин)-(3 ч+15 мин)==20 ч+49 мин-3 ч-15 мин=
=(20 ч-3 ч)+(49 мин-15 мин)=17 ч+34 мин=
=17 ч 34 мин - длится самый длинный день в Москве.
Ответ: 17 ч 34 мин.
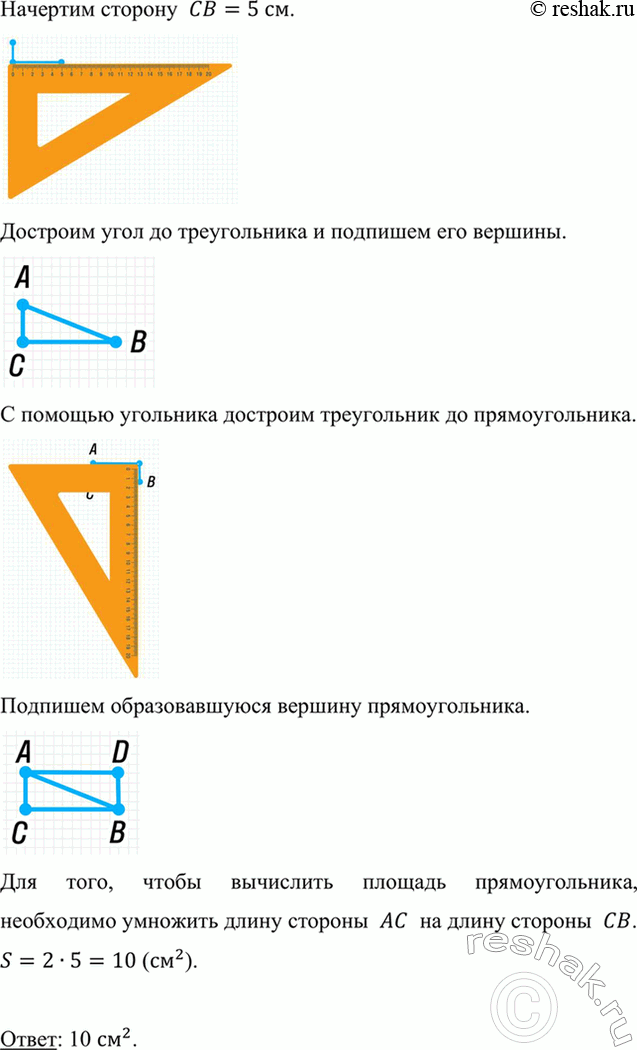
7. Начерти в тетради треугольник АВС так, чтобы угол АСВ был прямым, длина стороны АС была равна 2 см, а длина стороны СВ была равна 5 см. Дострой этот треугольник до прямоугольника и вычисли его площадь.
Для того, чтобы определить вид угла с помощью чертёжного треугольника, необходимо приложить одну из сторон прямого угла к стороне угла так, чтобы вершины углов совпадали. Если при этом другая сторона угла окажется:
- внутри треугольника, то этот угол острый;
- вне треугольника, то этот угол тупой;
- на стороне треугольника, то этот угол прямой.
С помощью треугольника начертим прямой угол ACB, в котором AC=2 см,CB=5 см.
Начертим сторону AC=2 см.
Начертим сторону CB=5 см.
Достроим угол до треугольника и подпишем его вершины.
С помощью угольника достроим треугольник до прямоугольника.
Подпишем образовавшуюся вершину прямоугольника.
Для того, чтобы вычислить площадь прямоугольника, необходимо умножить длину стороны AC на длину стороны CB.
S=2•5=10 ([см]^2).
Ответ: 10 [см]^2.
Похожие решебники
Популярные решебники 4 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением






