Упр.36.17 ГДЗ Мордковича 10 класс профильный уровень (Алгебра)
Решение #1


Решение #2(записки учителя)

Решение #3(записки школьника)
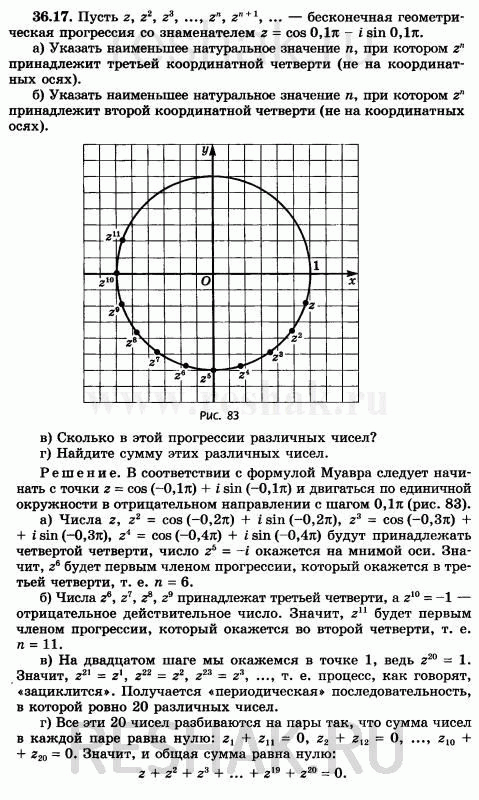

Рассмотрим вариант решения задания из учебника Мордкович, Семенов 10 класс, Мнемозина:
Пусть (z, z2, z3,... , zn, z(n+1),...} — бесконечная геометрическая прогрессия со знаменателем z = cos 0,1пи - i sin 0,1пи.
a) Укажите наименьшее натуральное значение n, при котором zn принадлежит третьей координатной четверти (не на координатных осях).
б) Укажите наименьшее натуральное значение n, при котором zn принадлежит второй координатной четверти (не на координатных осях).
в) Сколько в этой прогрессии различных чисел?
г) Найдите сумму этих различных чисел.
Похожие решебники
Популярные решебники 10 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением






