Упр.42.19 ГДЗ Мордковича 10 класс профильный уровень (Алгебра)
Решение #1
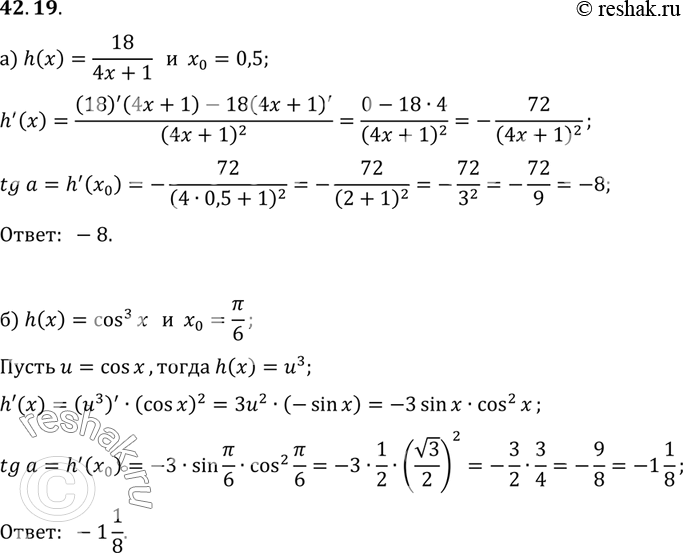
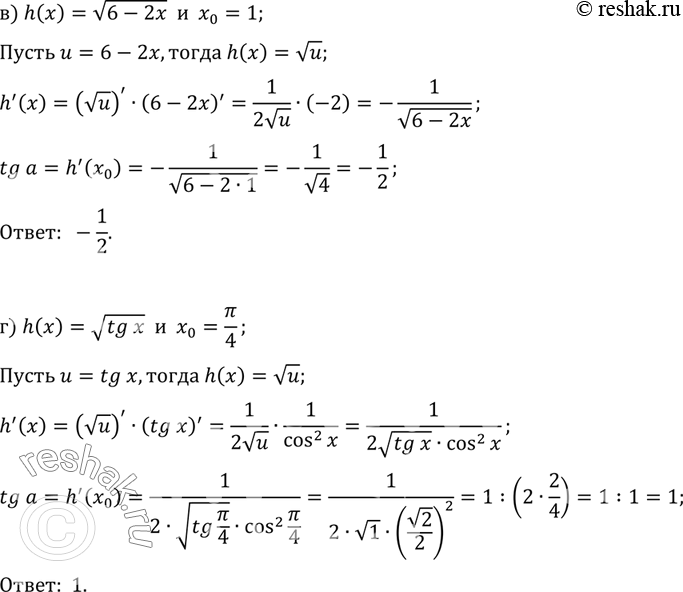
Решение #2(записки учителя)
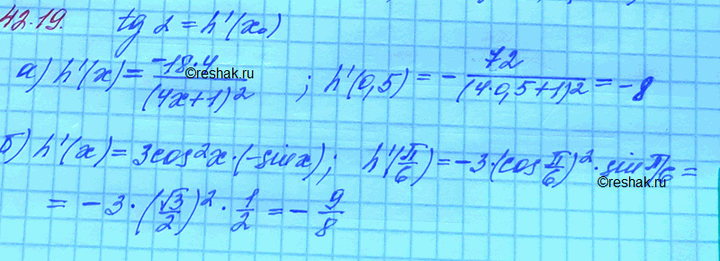
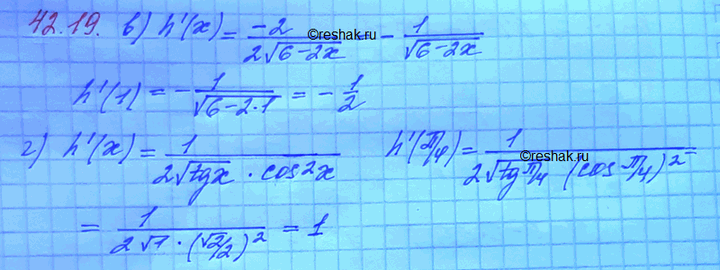
Решение #3(записки школьника)
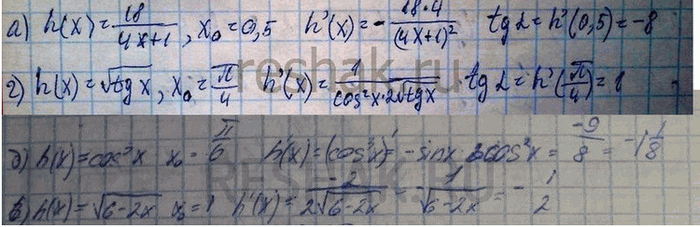
Решение #4
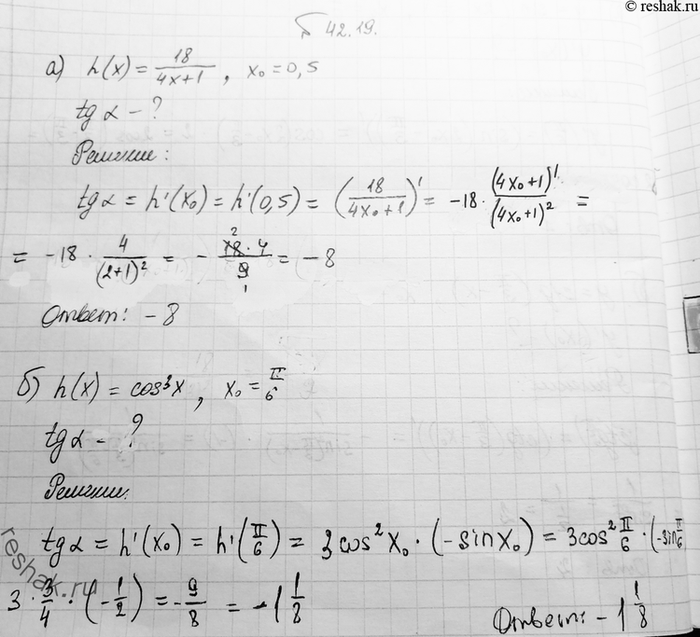

Рассмотрим вариант решения задания из учебника Мордкович, Семенов 10 класс, Мнемозина:
Найдите тангенс угла между касательной к графику функции у = h(x) в точке с абсциссой х0 и осью х:
a) h(x) = 18 /(4x + 1), х0 = 0,5;
б) h(x) = cos3 x, х0 = пи/6;
в) h(x) = корень(6 - 2х), х0 = 1;
г) h(x) = корень(tg x), х0 = пи/4.
Похожие решебники
Популярные решебники 10 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением






