Упр.10.10 ГДЗ Мордковича 11 класс профильный уровень (Алгебра)
Решение #1


Решение #2(записки учителя)

Решение #3(записки школьника)
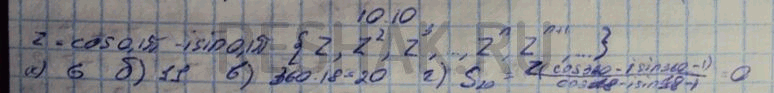

Рассмотрим вариант решения задания из учебника Мордкович, Семенов 11 класс, Мнемозина:
10.10. Пусть (z, z2, z3, ..., zn, zn + 1, ...) — геометрическая прогрессия со знаменателем z = cos0,1Пи - isin0,1Пи.
а) Укажите наименьшее натуральное значение n9 при котором zn лежит в третьей координатной четверти комплексной плоскости (не на координатных осях).
б) Укажите наименьшее натуральное значение n, при котором zn лежит во второй координатной четверти (не на координатных осях).
в) Сколько в этой прогрессии различных чисел?
г) Найдите сумму этих различных чисел.
Похожие решебники
Популярные решебники 11 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







