Упр.10.23 ГДЗ Мордкович Семенов 11 класс (Алгебра)
Решение #1
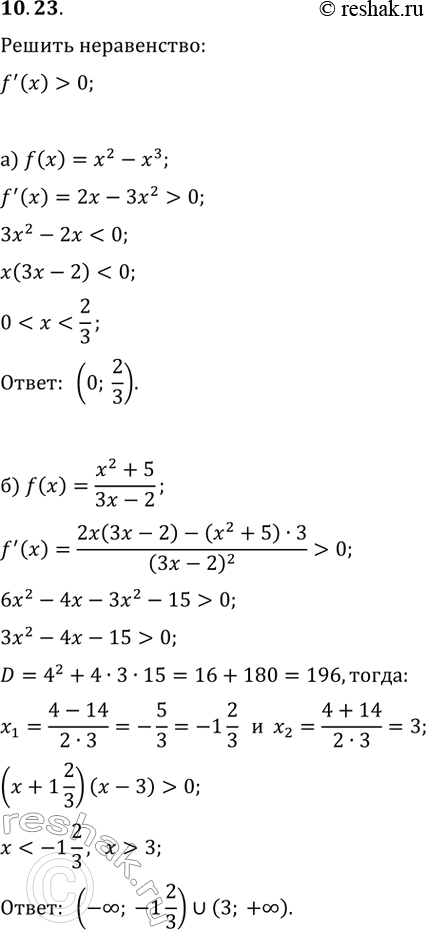
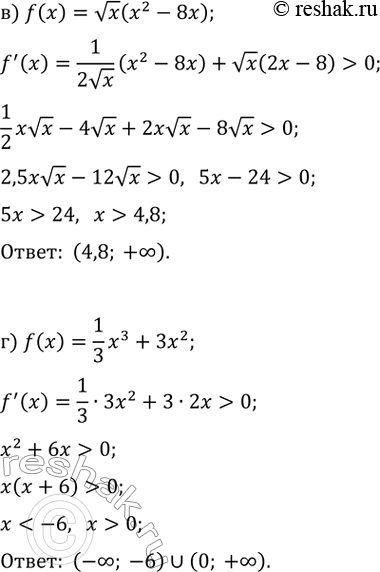
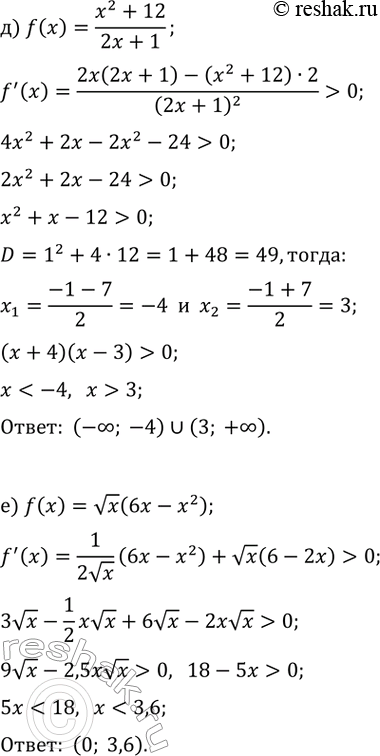

Рассмотрим вариант решения задания из учебника Мордкович, Семенов, Александрова 11 класс, Просвещение:
10.23. Решите неравенство f'(x) > 0, если:
а) f(x)=x^2-x^3; г) f(x)=(1/3)x^3+3x^2;
б) f(x)=(x^2+5)/(3x-2); д) f(x)=(x^2+12)/(2x+1);
в) f(x)=vx(x^2-8x); е) f(x)=vx(6x-x^2).
Похожие решебники
Популярные решебники 11 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







