Упр.2.212 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
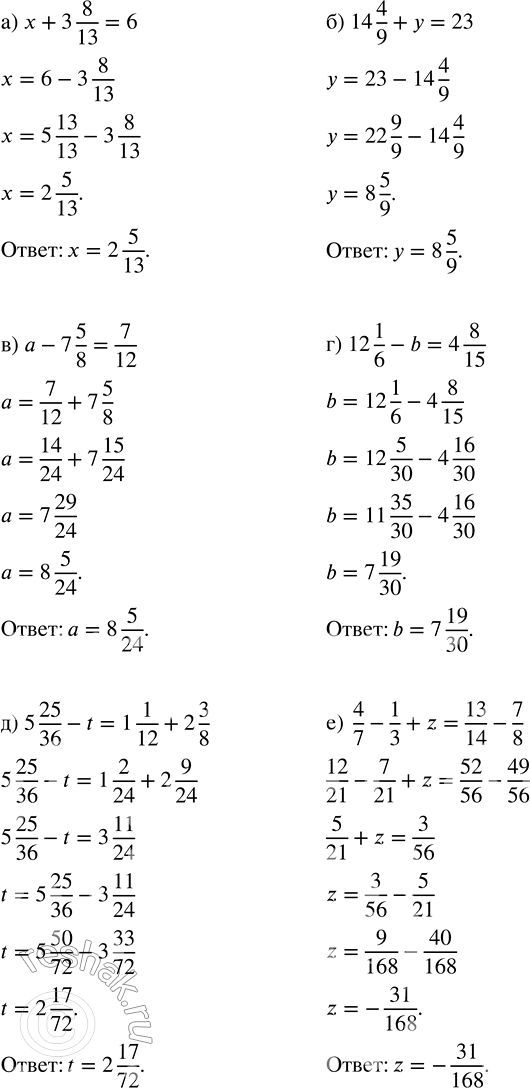
Решение #2 (Учебник 2023)


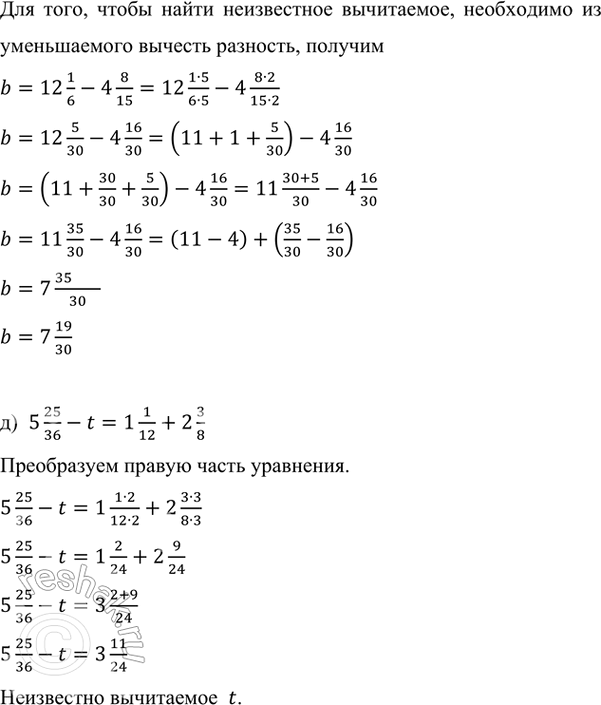

Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)
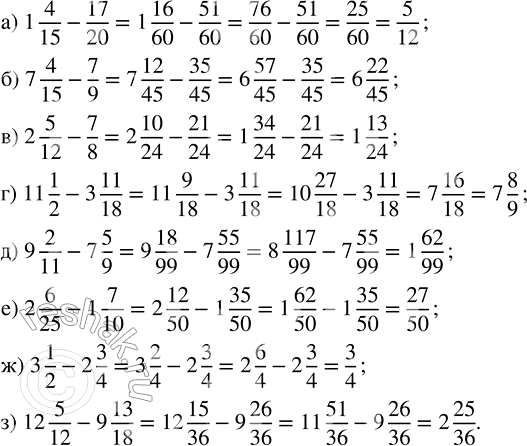
Решение #5 (Учебник 2021)

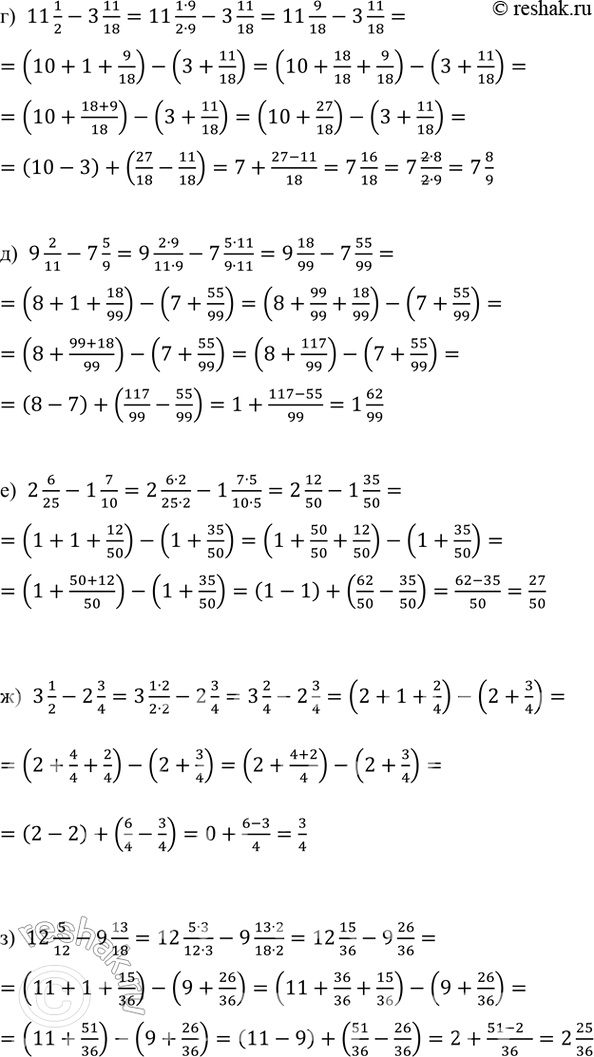
Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите корень уравнения:
а) x + 3 8/13 = 6; в) a - 7 5/8 = 7/12; д) 5 25/36 - t = 1 1/12 + 2 3/8;
б) 14 4/9 + y = 23; г) 12 1/6 - b = 4 8/15; е) 4/7 - 1/3 + z = 13/14 - 7/8.
Для того, чтобы выполнить сложение (вычитание) смешанных чисел, необходимо дробные части привести к общему знаменателю, затем отдельно выполнить сложение (вычитание) целых частей и дробных частей.
Если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится дробь равная данной.
Когда на первом месте стоит целое число и из него необходимо вычесть смешанное число, нужно целое число представить в виде смешанного числа, у которого дробная часть будет являться неправильной дробью.
Если в первом числителе стоит число меньше, чем во втором числителе, то необходимо занять единицу у целой части и представить её в виде неправильной дроби совместно с данной дробью, затем отдельно выполнить вычитание целых частей и дробных частей.
а) x+3 8/13=6
Неизвестно слагаемое x.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим
x=6-3 8/13
x=(5+1)-3 8/13=5 13/13-3 8/13
x=(5-3)+(13/13-8/13)=2+(13-8)/13
x=2 5/13
б) 14 4/9+y=23
Неизвестно слагаемое y.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим
y=23-14 4/9
y=(22+1)-14 4/9=22 9/9-14 4/9
y=(22-14)+(9/9-4/9)=8+(9-4)/9
y=8 5/9
в) a-7 5/8=7/12
Неизвестно уменьшаемое a.
Для того, чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое, получим
a=7/12+7 5/8
a=(7•2)/(12•2)+7 (5•3)/(8•3)=14/24+7 15/24
a=7+(14/24+15/24)=7 (14+15)/24
a=7 29/24=7+1 5/24
a=8 5/24
г) 12 1/6-b=4 8/15
Неизвестно вычитаемое b.
Для того, чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность, получим
b=12 1/6-4 8/15=12 (1•5)/(6•5)-4 (8•2)/(15•2)
b=12 5/30-4 16/30=(11+1+5/30)-4 16/30
b=(11+30/30+5/30)-4 16/30=11 (30+5)/30-4 16/30
b=11 35/30-4 16/30=(11-4)+(35/30-16/30)
b=7 (35-16)/30
b=7 19/30
д) 5 25/36-t=1 1/12+2 3/8
Преобразуем правую часть уравнения.
5 25/36-t=1 (1•2)/(12•2)+2 (3•3)/(8•3)
5 25/36-t=1 2/24+2 9/24
5 25/36-t=3 (2+9)/24
5 25/36-t=3 11/24
Неизвестно вычитаемое t.
Для того, чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность, получим
t=5 25/36-3 11/24=5 (25•2)/(36•2)-3 (11•3)/(24•3)
t=5 50/72-3 33/72=(5-3)+(50/72-33/72)
t=2+(50-33)/72
t=2 17/72
е) 4/7-1/3+z=13/14-7/8
Преобразем уравнение.
(4•3)/(7•3)-(1•7)/(3•7)+z=(13•4)/(14•4)-(7•7)/(8•7)
12/21-7/21+z=52/56-49/56
(12-7)/21+z=(52-49)/56
5/21+z=3/56
Неизвестно слагаемое z.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим
z=3/56-5/21=(3•3)/(56•3)-(5•8)/(21•8)
z=9/168-40/168=(9-40)/168
z=-31/168
Выполните действие:
а) 1 4/15 - 17/20; в) 2 5/12 - 7/8; д) 9 2/11 - 7 5/9; ж) 3 1/2 - 2 3/4;
б) 7 4/15 - 7/9; г) 11 1/2 - 3 11/18; е) 2 6/25 - 1 7/10; з) 12 5/12 - 9 13/18.
Для того, чтобы выполнить вычитание смешанных чисел, необходимо дробные части привести к общему знаменателю, затем отдельно выполнить вычитание целых частей и дробных частей.
Если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится дробь равная данной.
Если в первом числителе стоит число меньше, чем во втором числителе, то необходимо занять единицу у целой части и представить её в виде неправильной дроби совместно с данной дробью, затем отдельно выполнить вычитание целых частей и дробных частей.
Если в ответе получается сократимая дробь, необходимо числитель и знаменатель разделить на одно и то же число.
а) 1 4/15-17/20=1 (4•4)/(15•4)-(17•3)/(20•3)=1 16/60-51/60=(1+16/60)-51/60=(60/60+16/60)-51/60=(60+16)/60-51/60=76/60-51/60=(76-51)/60=25/60=(5•5)/(5•12)=5/12
б) 7 4/15-7/9=7 (4•3)/(15•3)-(7•5)/(9•5)=7 12/45-35/45=(6+1+12/45)-35/45=(6+45/45+12/45)-35/45=(6+(45+12)/45)-35/45=(6+57/45)-35/45=(6-0)+(57/45-35/45)=6+(57-35)/45=6 22/45
в) 2 5/12-7/8=2 (5•2)/(12•2)-(7•3)/(8•3)=2 10/24-21/24=(1+1+10/24)-21/24=(1+24/24+10/24)-21/24=(1+(24+10)/24)-21/24=(1+34/24)-21/24=(1-0)+(34/24-21/24)=1+(34-21)/24=1 13/24
г) 11 1/2-3 11/18=11 (1•9)/(2•9)-3 11/18=11 9/18-3 11/18=(10+1+9/18)-(3+11/18)=(10+18/18+9/18)-(3+11/18)=(10+(18+9)/18)-(3+11/18)=(10+27/18)-(3+11/18)=(10-3)+(27/18-11/18)=7+(27-11)/18=7 16/18=7 (2•8)/(2•9)=7 8/9
д) 9 2/11-7 5/9=9 (2•9)/(11•9)-7 (5•11)/(9•11)=9 18/99-7 55/99=(8+1+18/99)-(7+55/99)=(8+99/99+18/99)-(7+55/99)=(8+(99+18)/99)-(7+55/99)=(8+117/99)-(7+55/99)=(8-7)+(117/99-55/99)=1+(117-55)/99=1 62/99
е) 2 6/25-1 7/10=2 (6•2)/(25•2)-1 (7•5)/(10•5)=2 12/50-1 35/50=(1+1+12/50)-(1+35/50)=(1+50/50+12/50)-(1+35/50)=(1+(50+12)/50)-(1+35/50)=(1-1)+(62/50-35/50)=(62-35)/50=27/50
ж) 3 1/2-2 3/4=3 (1•2)/(2•2)-2 3/4=3 2/4-2 3/4=(2+1+2/4)-(2+3/4)=(2+4/4+2/4)-(2+3/4)=(2+(4+2)/4)-(2+3/4)=(2-2)+(6/4-3/4)=0+(6-3)/4=3/4
з) 12 5/12-9 13/18=12 (5•3)/(12•3)-9 (13•2)/(18•2)=12 15/36-9 26/36=(11+1+15/36)-(9+26/36)=(11+36/36+15/36)-(9+26/36)=(11+51/36)-(9+26/36)=(11-9)+(51/36-26/36)=2+(51-26)/36=2 25/36
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







