Упр.2.294 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)

Решение #5 (Учебник 2021)

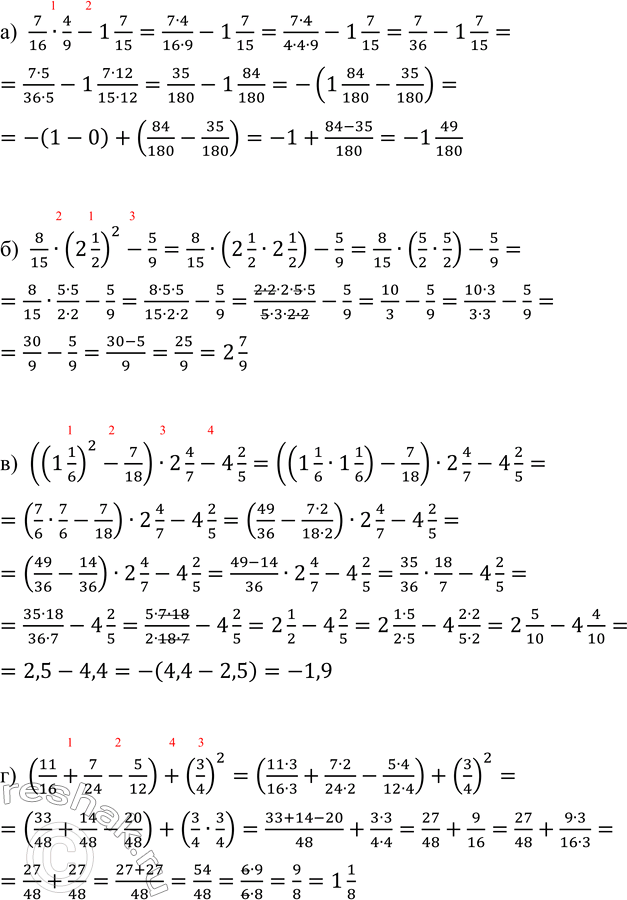
Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Сколько граммов составляют:
а) 1 % килограмма; б) 9 % килограмма; в) 90 % килограмма; г) 7,5 % килограмма?
2.306. Сколько квадратных метров составляют:
а) 1 % ара; в) 35 % гектара;
б) 5,5 % сотки; г) 0,06 % квадратного километра?
Напомним, что 1 кг=1 000 г.
Для того, чтобы найти несколько процентов от числа, необходимо это число разделить на 100, то есть найти 1% от числа, а затем, полученный результат, умножить на число, стоящее перед знаком %.
а) 1% кг=1000 г:100•1=10 г•1=10 г.
б) 9% кг=1000 г:100•9=10 г•9=90 г.
в) 90% кг=1000 г:100•90=10 г•90=900 г.
г) 7,5% кг=1000 г:100•7,5=10 г•7,5=75 г.
Вычислите:
а) 7/16 · 4/9 - 1 7/15; в) ((1 1/6)^2 - 7/18) · 2 4/7 - 4 2/5;
б) 8/15 · (2 1/2)^2 - 5/9; г) (11/16 + 7/24 - 5/12) + (3/4)^2.
Если в выражении есть скобки, то сначала выполняют действия в скобках.
Для того, чтобы выполнить сложение (вычитание) смешанных чисел, необходимо дробные части привести к общему знаменателю, затем отдельно выполнить сложение (вычитание) целых частей и дробных частей.
При умножении числителя и знаменателя дроби на одно и то же число, получается дробь равная данной.
Если при вычитании в первом числителе стоит число меньше, чем во втором числителе, то необходимо занять единицу у целой части и представить её в виде неправильной дроби совместно с данной дробью, затем отдельно выполнить вычитание целых частей и дробных частей.
Для того, чтобы умножить дробь на дробь, необходимо найти произведение числителей и знаменателей этих дробей. Первое произведение записать числителем, второе – знаменателем.
В примерах даны смешанные числа, которые сначала необходимо представить в виде неправильных дробей, для этого нужно знаменатель умножить на целую часть и к полученному результату прибавить числитель, затем, то, что получили, записываем в числитель, знаменатель останется тот же.
При умножении необходимо выполнять сокращение, если это возможно, для удобства расчётов. Для этого необходимо одно из чисел числителя и знаменателя разделить на одно и то же число и далее выполнять умножение.
При возведении в степень дроби, данную дробь необходимо умножить на саму себя столько раз, какова степень числа.
а) 7/16•4/9-1 7/15=(7•4)/(16•9)-1 7/15=(7•4)/(4•4•9)-1 7/15=7/36-1 7/15=(7•5)/(36•5)-1 (7•12)/(15•12)=35/180-1 84/180=-(1 84/180-35/180)=-(1-0)+(84/180-35/180)=-1+(84-35)/180=-1 49/180
б) 8/15•(2 1/2)^2-5/9=8/15•(2 1/2•2 1/2)-5/9=8/15•(5/2•5/2)-5/9=8/15•(5•5)/(2•2)-5/9=(8•5•5)/(15•2•2)-5/9=(2•2•2•5•5)/(5•3•2•2)-5/9=10/3-5/9=(10•3)/(3•3)-5/9=30/9-5/9=(30-5)/9=25/9=2 7/9
в) ((1 1/6)^2-7/18)•2 4/7-4 2/5=((1 1/6•1 1/6)-7/18)•2 4/7-4 2/5=(7/6•7/6-7/18)•2 4/7-4 2/5=(49/36-(7•2)/(18•2))•2 4/7-4 2/5=(49/36-14/36)•2 4/7-4 2/5=(49-14)/36•2 4/7-4 2/5=35/36•18/7-4 2/5=(35•18)/(36•7)-4 2/5=(5•7•18)/(2•18•7)-4 2/5=2 1/2-4 2/5=2 (1•5)/(2•5)-4 (2•2)/(5•2)=2 5/10-4 4/10=2,5-4,4=-(4,4-2,5)=-1,9
г) (11/16+7/24-5/12)+(3/4)^2=((11•3)/(16•3)+(7•2)/(24•2)-(5•4)/(12•4))+(3/4)^2=(33/48+14/48-20/48)+(3/4•3/4)=(33+14-20)/48+(3•3)/(4•4)=27/48+9/16=27/48+(9•3)/(16•3)=27/48+27/48=(27+27)/48=54/48=(6•9)/(6•8)=9/8=1 1/8
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







