Упр.2.32 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
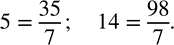
Решение #2 (Учебник 2023)

Решение #3 (Учебник 2021)
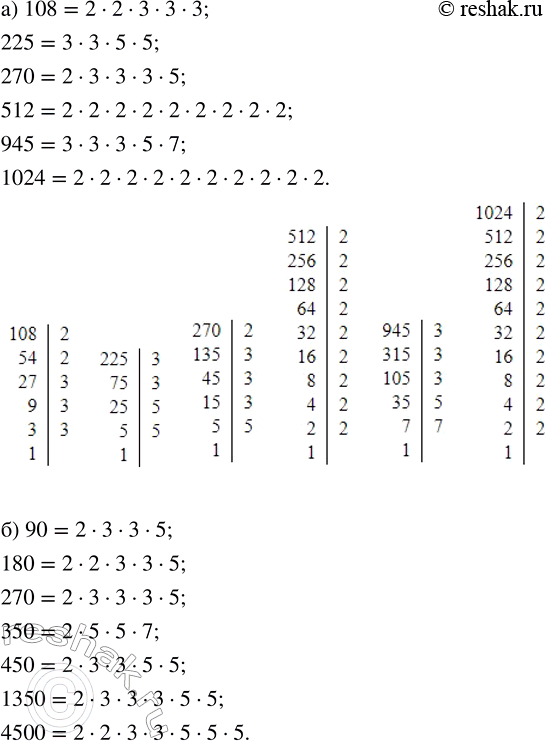
Решение #4 (Учебник 2021)

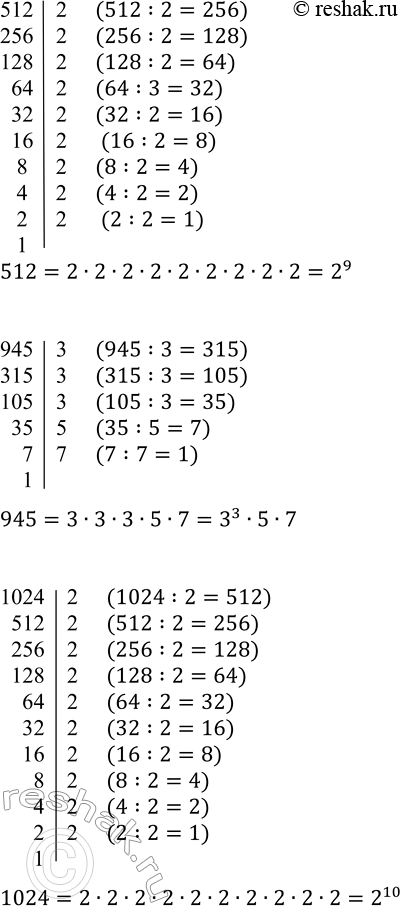



Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Представьте в виде дроби со знаменателем 7 числа 5 и 14.
Любое натуральное число можно записать в виде дроби с любым натуральным знаменателем.
Числитель этой дроби равен произведению числа и этого знаменателя.
Для того, чтобы записать число 5 в виде дроби со знаменателем 7, необходимо найти число, при делении которого на 7 получилось бы 5.
Это число 5•7.
Значит, число 5 можно записать в виде дроби
5=(5•7)/7=35/7
Для того, чтобы записать число 14 в виде дроби со знаменателем 7, необходимо найти число, при делении которого на 7 получилось бы 14.
Это число 14•7.
Значит, число 14 можно записать в виде дроби
14=(14•7)/7=98/7
Разложите на простые множители числа:
а) 108, 225, 270, 512, 945, 1024; в) 13, 2002, 1225, 14 014, 90 720.
б) 90, 180, 270, 350, 450, 1350, 4500;
Представление числа в виде произведения его простых делителей, называют разложением числа на простые множители.
Любое составное число можно разложить на простые множители.
Признаки делимости помогают при разложении числа на простые множители.
При этом запись удобно вести с помощью вертикальной черты.
а) 108, 225, 270, 512, 945, 1024
108 2 (108:2=54)
54 2 (54:2=27)
27 3 (27:3=9)
9 3 (9:3=3)
3 3 (3:3=1)
1
108=2•2•3•3•3=2^2•3^3
225 3 (225:3=75)
75 3 (75:3=25)
25 5 (25:5=5)
5 5 (5:5=1)
1
225=3•3•5•5=3^2•5^2
270 2 (270:2=135)
135 3 (135:3=45)
45 3 (45:3=15)
15 3 (15:3=5)
5 5 (5:5=1)
1
270=2•3•3•3•5=2•3^3•5
512 2 (512:2=256)
256 2 (256:2=128)
128 2 (128:2=64)
64 2 (64:3=32)
32 2 (32:2=16)
16 2 (16:2=8)
8 2 (8:2=4)
4 2 (4:2=2)
2 2 (2:2=1)
1
512=2•2•2•2•2•2•2•2•2=2^9
945 3 (945:3=315)
315 3 (315:3=105)
105 3 (105:3=35)
35 5 (35:5=7)
7 7 (7:7=1)
1
945=3•3•3•5•7=3^3•5•7
1024 2 (1024:2=512)
512 2 (512:2=256)
256 2 (256:2=128)
128 2 (128:2=64)
64 2 (64:2=32)
32 2 (32:2=16)
16 2 (16:2=8)
8 2 (8:2=4)
4 2 (4:2=2)
2 2 (2:2=1)
1
1024=2•2•2•2•2•2•2•2•2•2=2^10
б) 90, 180, 270, 350, 450, 1350, 4500
90 2 (90:2=45)
45 3 (45:3=15)
15 3 (15:3=5)
5 5 (5:5=1)
1
90=2•3•3•5=2•3^2•5
180 2 (180:2=90)
90 2 (90:2=45)
45 3 (45:3=15)
15 3 (15:3=5)
5 5 (5:5=1)
1
180=2•2•3•3•5=2^2•3^2•5
270 2 (270:2=135)
135 3 (135:3=45)
45 3 (45:3=15)
15 3 (15:3=5)
5 5 (5:5=1)
1
270=2•3•3•3•5=2•3^3•5
350 2 (350:2=175)
175 5 (175:5=35)
35 5 (35:5=7)
7 7 (7:7=1)
1
350=2•5•5•7=2•5^2•7
450 2 (450:2=225)
225 3 (225:3=75)
75 3 (75:3=25)
25 5 (25:5=5)
5 5 (5:5=1)
1
450=2•3•3•5•5=2•3^2•5^2
1350 2 (1350:2=675)
675 3 (675:3=225)
225 3 (225:3=75)
75 3 (75:3=25)
25 5 (25:5=5)
5 5 (5:5=1)
1
1350=2•3•3•3•5•5=2•3^3•5^2
4500 2 (4500:2=2250)
2250 2 (2250:2=1125)
1125 3 (1125:3=375)
375 3 (375:3=125)
125 5 (125:5=25)
25 5 (25:5=5)
5 5 (5:5=1)
1
4500=2•2•3•3•5•5•5=2^2•3^2•5^3
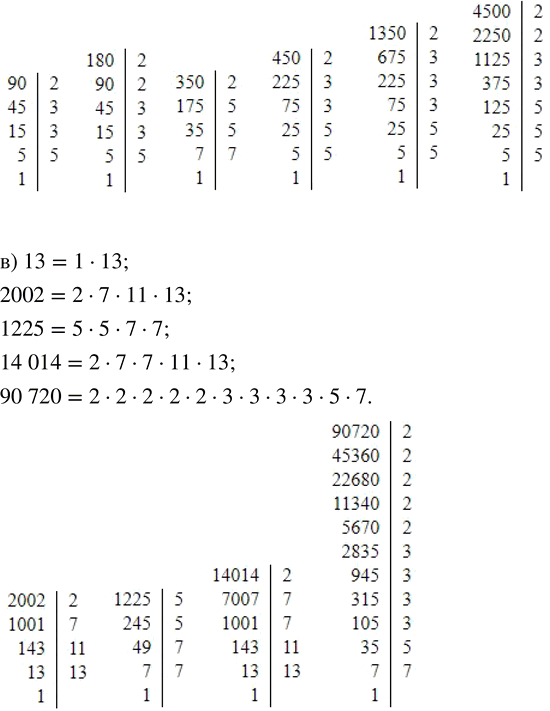
в) 13, 2002, 1225, 14014, 90720
13 – простое число.
Разложение числа 13 на множители 1 и 13 (13=1•13) не является разложением на простые множители.
2002 2 (2002:2=1001)
1001 7 (1001:7=143)
143 11 (143:11=13)
13 13 (13:13=1)
1
2002=2•7•11•13
1225 5 (1225:5=245)
245 5 (245:5=49)
49 7 (49:7=7)
7 7 (7:7=1)
1
1225=5•5•7•7=5^2•7^2
14014 2 (14014:2=7007)
7007 7 (7007:7=1001)
1001 7 (1001:7=143)
143 11 (143:11=13)
13 13 (13:13=1)
1
14014=2•7•7•11•13=2•7^2•11•13
90720 2 (90720:2=45360)
45360 2 (45360:2=22680)
22680 2 (22680:2=11340)
11340 2 (11340:2=5670)
5670 2 (5670:2=2835)
2835 3 (2835:3=945)
945 3 (945:3=315)
315 3 (315:3=105)
105 3 (105:3=35)
35 5 (35:5=7)
7 7 (7:7=1)
1
90720=2•2•2•2•2•3•3•3•3•5•7=2^5•3^4•5•7
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







