Упр.2.416 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)
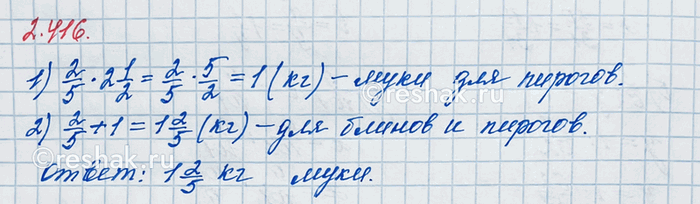
Решение #4 (Учебник 2021)
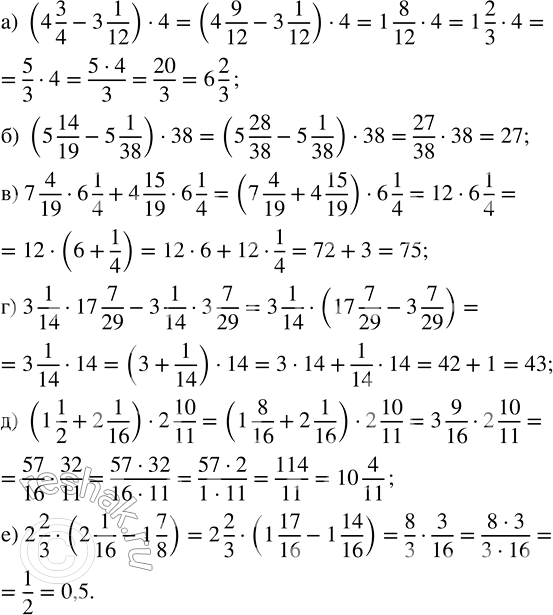
Решение #5 (Учебник 2021)

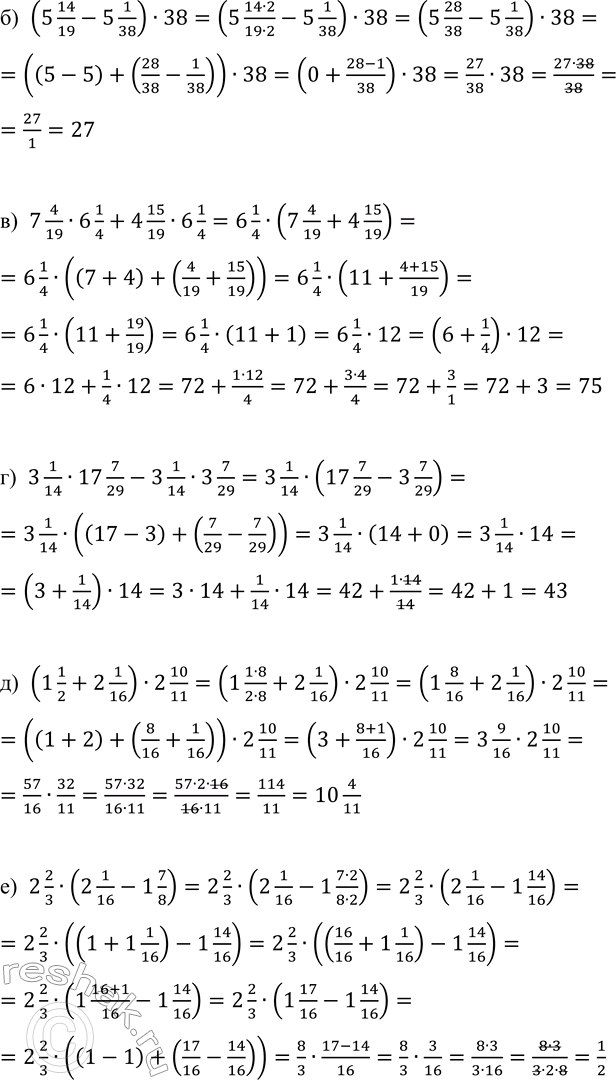
Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Для приготовления блинов потребовалось 2/5 кг муки, а для выпечки пирогов в 2 1/2 раза больше. Сколько муки потребовалось для выпечки блинов и пирогов вместе?
По условию для приготовления блинов потребовалось 2/5 кг муки, а для выпечки пирогов в 2 1/2 раза больше муки, чем для блинов.
Значит, чтобы найти, сколько муки потребовалось для выпечки пирогов, необходимо количество муки для приготовления блинов умножить на 2 1/2 , то есть для выпечки пирогов потребовалось
2/5•2 1/2=2/5•5/2=(2•5)/(5•2)=1/1=1 (кг) – муки.
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
Смешанные числа перед умножением необходимо представить в виде неправильных дробей.
Для того, чтобы записать смешанное число в виде неправильной дроби, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
При этом, прежде, чем перемножить числа, выполняем сокращение.
Для того, чтобы найти, сколько муки потребовалось для выпечки блинов и пирогов вместе, необходимо сложить количество муки для блинов и количество муки для пирогов, то есть
2/5+1=1 2/5=1 (2•2)/(5•2)=1 4/10=1,4 (кг) – муки потребовалось.
Ответ: 1,4 кг.
Вычислите:
а) (4 3/4 - 3 1/12) · 4; в) 7 4/19 · 6 1/4 + 4 15/19 · 6 1/4; д) (1 1/2 + 2 1/16) · 2 10/11;
б) (5 14/19 - 5 1/38) · 38; г) 3 1/14 · 17 7/29 - 3 1/14 · 3 7/29; е) 2 2/3 · (2 1/16 - 1 7/8).
При выполнении вычислений опираемся на следующие правила:
- произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
- для того, чтобы выполнить умножение смешанных чисел, необходимо записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
- для того, чтобы записать смешанное число в виде неправильной дроби, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
- для того, чтобы сложить (вычесть) дроби с разными знаменателями, необходимо сначала привести эти дроби к наименьшему общему знаменателю (используя дополнительные множители), а затем сложить (вычесть) их числители, а знаменатель оставить прежним.
Прежде, чем перемножать числа, сокращаем их.
Для того, чтобы умножить смешанное число на натуральное число, можно умножить целую часть на натуральное число, далее умножить дробную часть на это натуральное число и полученные произведения сложить.
а) (4 3/4-3 1/12)•4=(4 (3•3)/(4•3)-3 1/12)•4=(4 9/12-3 1/12)•4=((4-3)+(9/12-1/12))•4=(1+(9-1)/12)•4=(1+8/12)•4=1•4+8/12•4=4+(8•4)/12=4+(8•4)/(3•4)=4+8/3=4+2 2/3=6 2/3
б) (5 14/19-5 1/38)•38=(5 (14•2)/(19•2)-5 1/38)•38=(5 28/38-5 1/38)•38=((5-5)+(28/38-1/38))•38=(0+(28-1)/38)•38=27/38•38=(27•38)/38==27/1=27
в) 7 4/19•6 1/4+4 15/19•6 1/4=6 1/4•(7 4/19+4 15/19)=6 1/4•((7+4)+(4/19+15/19))=6 1/4•(11+(4+15)/19)=6 1/4•(11+19/19)=6 1/4•(11+1)=6 1/4•12=(6+1/4)•12=6•12+1/4•12=72+(1•12)/4=72+(3•4)/4=72+3/1=72+3=75
г) 3 1/14•17 7/29-3 1/14•3 7/29=3 1/14•(17 7/29-3 7/29)=3 1/14•((17-3)+(7/29-7/29))=3 1/14•(14+0)=3 1/14•14=(3+1/14)•14=3•14+1/14•14=42+(1•14)/14=42+1=43
д) (1 1/2+2 1/16)•2 10/11=(1 (1•8)/(2•8)+2 1/16)•2 10/11=(1 8/16+2 1/16)•2 10/11=((1+2)+(8/16+1/16))•2 10/11=(3+(8+1)/16)•2 10/11=3 9/16•2 10/11=57/16•32/11=(57•32)/(16•11)=(57•2•16)/(16•11)=114/11=10 4/11
е) 2 2/3•(2 1/16-1 7/8)=2 2/3•(2 1/16-1 (7•2)/(8•2))=2 2/3•(2 1/16-1 14/16)=2 2/3•((1+1 1/16)-1 14/16)=2 2/3•((16/16+1 1/16)-1 14/16)=2 2/3•(1 (16+1)/16-1 14/16)=2 2/3•(1 17/16-1 14/16)=2 2/3•((1-1)+(17/16-14/16))=8/3•(17-14)/16=8/3•3/16=(8•3)/(3•16)=(8•3)/(3•2•8)=1/2
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







