Упр.2.471 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)


Решение #3 (Учебник 2023)
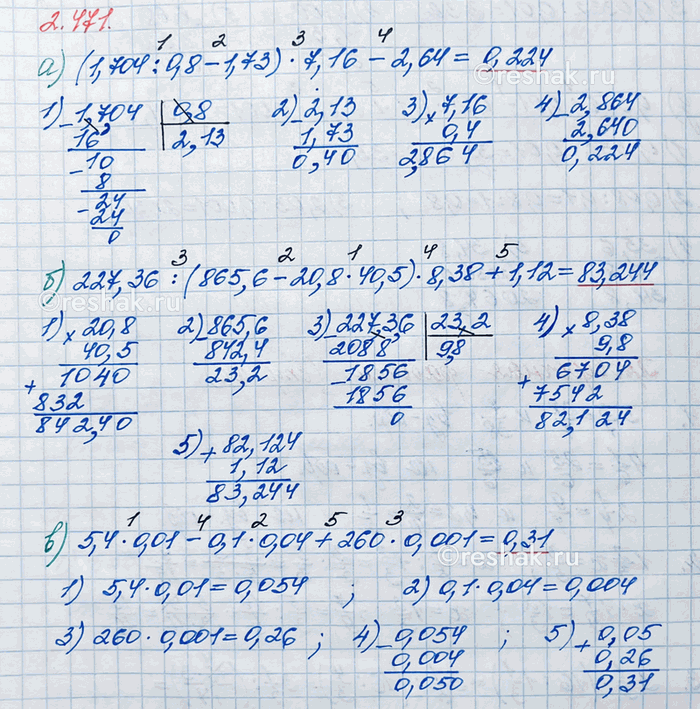
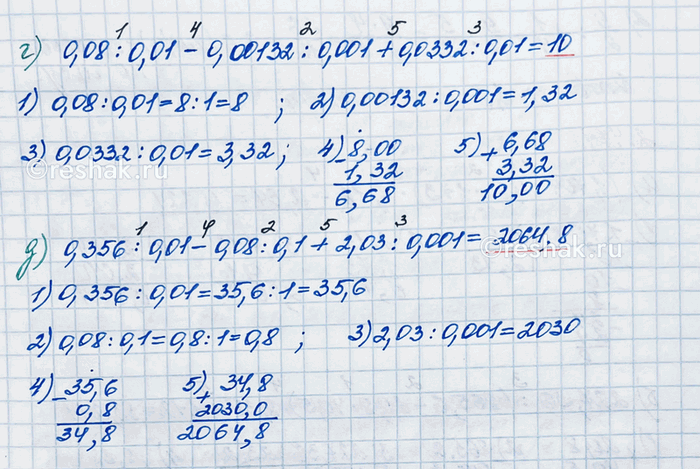
Решение #4 (Учебник 2021)
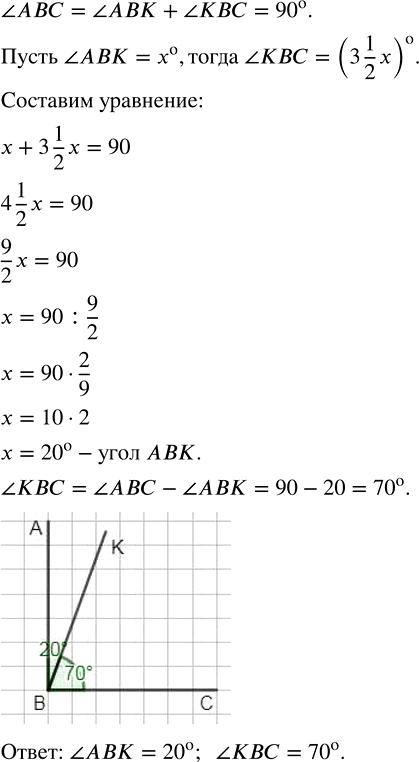
Решение #5 (Учебник 2021)



Решение #6 (Учебник 2021)
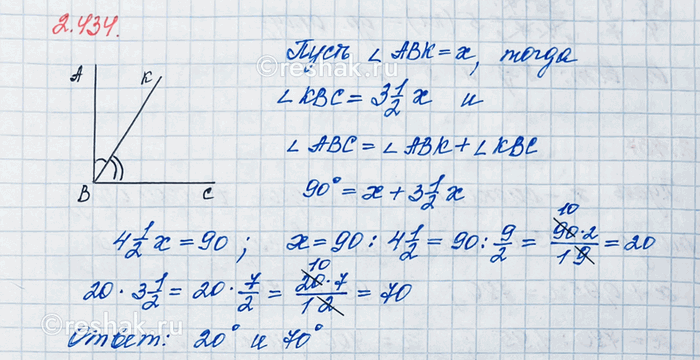
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите значение выражения:
а) (1,704 : 0,8 - 1,73) · 7,16 - 2,64;
б) 227,36 : (865,6 - 20,8 · 40,5) · 8,38 + 1,12;
в) 5,4 · 0,01 - 0,1 · 0,04 + 260 · 0,001;
г) 0,08 : 0,01 - 0,00132 : 0,001 + 0,0332 : 0,01;
д) 0,356 : 0,01 - 0,08 : 0,1 + 2,03 : 0,001.
Порядок выполнения действий выбираем согласно следующим правилам:
- если в выражении нет скобок, и оно содержит действия первой и второй ступени, то сначала выполняют действия второй ступени (умножение и деление) по порядку слева направо, а потом действия первой ступени (сложение и вычитание), также по порядку слева направо.
- если в выражении есть скобки, то сначала выполняют действия в скобках, а затем за скобками; и в скобках, и за скобками сначала выполняют действия второй ступени, а затем действия первой ступени, по порядку слева направо.
При вычислениях опираемся на следующие правила:
- для того, чтобы разделить десятичную дробь на 0,1, 0,01, 0,001 и так далее, необходимо в этой дроби перенести запятую вправо соответственно на 1, 2, 3 и так далее цифры.
- для того, чтобы умножить десятичную дробь на 0,1, 0,01, 0,001 и так далее, необходимо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и так далее цифры.
- для того, чтобы разделить десятичную дробь на натуральное число, необходимо разделить дробь на это число, не обращая внимание на запятую; поставить в частном запятую, когда кончится деление целой части.
- для того, чтобы разделить десятичную дробь на десятичную, необходимо перенести в делимом и делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе; выполнить деление на натуральное число.
а) (1,704:0,8-1,73)•7,16-2,64=(17,04:8-1,73)•7,16-2,64=(2,13-1,73)•7,16-2,64=0,4•7,16-2,64=2,864-2,64=0,224
б) 227,36:(865,6-20,8•40,5)•8,38+1,12=227,36:(865,6-842,4)•8,38+1,12=227,36:23,2•8,38+1,12=2273,6:232•8,38+1,12=9,8•8,38+1,12=82,124+1,12=83,244
в) 5,4•0,01-0,1•0,04+260•0,001=0,054-0,004+0,26==0,05+0,26=0,31
г) 0,08:0,01-0,00132:0,001+0,0332:0,01=8-1,32+3,32=6,68+3,32=10
д) 0,356:0,01-0,08:0,1+2,03:0,001=35,6-0,8+2030=34,8+2030=2064,8
Прямой угол АВС луч ВК делит на углы АВК и КВС. Угол AВК меньше угла КВС в 3 1/2 раза. Найдите градусные меры углов AВК и КВС. Постройте эти углы.
Углы находим при помощи уравнения.
Луч BK делит прямой угол ABC, то есть равный 90°, на два угла ABK и KBC.
Пусть угол ABK равен x, тогда угол KBC равен 3 1/2 x, так как угол ABK меньше угла KBC в 3 1/2 раза.
Следовательно, можно составить следующее уравнение
x+3 1/2 x=90, или, учитывая то, что при умножении единицы на любое число, получим равное ему число, можно записать
1•x+3 1/2 x=90
Далее преобразуем полученное уравнение, используя распределительное свойство умножения относительно сложения, то есть выносим одинаковый множитель x за скобки, получим
(1+3 1/2)x=90
Для того, чтобы найти сумму двух смешанных чисел, необходимо отдельно сложить их целые и дробные части.
Тогда, выполнив сложение в скобках, получим
4 1/2 x=90
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=90:4 1/2
Для того, чтобы выполнить деление, сначала представим смешанное число 4 1/2 в виде неправильной дроби.
Для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части, эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа, получим
4 1/2=9/2 , так как 4•2+1=8+1=9 .
Тогда, x=90:9/2 .
Для того, чтобы разделить натуральное число на обыкновенную дробь, необходимо делимое умножить на число, обратное делителю, то есть у делителя поменять местами числитель и знаменатель, получим
x=90•2/9
Для того, чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменений, тогда
x=(90•2)/9=(9•10•2)/9
Или, выполнив сокращение,
x=(10•2)/1 , или, выполнив умножение в числителе,
x=20/1 .
Дробь, у которой в знаменателе стоит единица, равна числителю.
Значит, x=20°.
Следовательно, угол ABK=20°.
Прямой угол равен 90°, один из углов (угол ABK) равен 20°, значит, угол KBC=90°-20°=70°.
Сначала построим угол ABC, равный 90°.
Для этого чертим с помощью линейки луч AB.
Далее совмещаем начало B луча AB с центром транспортира, при этом луч AB должен пройти через нулевое деление внешней шкалы транспортира, далее на внешней шкале транспортира ищем деление 90° и ставим напротив этого деления точку C.
Затем проводим луч BC и получаем угол ABC=90°.
Теперь построим луч BK так, что угол ABK=20°, а угол KBC=70°.
Для этого совмещаем вершину B угла ABC с центром транспортира, при этом сторона AB этого угла должна пройти через нулевое деление внешней шкалы транспортира.
Далее на внешней стороне шкалы транспортира ищем деление 20° и ставим напротив этого деления точку K.
Затем проводим луч BK и получаем угол ABK=20° и
угол KBC=70°.
Ответ: 20° и 70°.
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







