Упр.2.486 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)
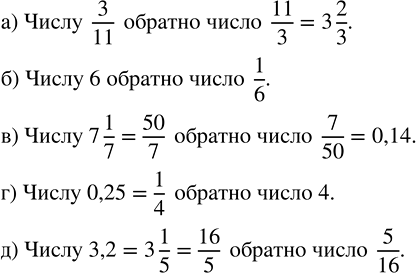
Решение #5 (Учебник 2021)


Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Бригада железнодорожников в первый день отремонтировала 2/9 всего участка пути, во второй день — 4/7 оставшегося участка пути, а в третий — остальные 6 км. Сколько километров пути отремонтировала бригада за три дня?
Весь путь – это 1.
По условию, в первый день бригада отремонтировала 2/9 части пути.
Значит, осталось отремонтировать 1-2/9=9/9-2/9=(9-2)/9=7/9 части пути.
Также известно, что во второй день бригада отремонтировала 4/7 оставшегося участка пути, то есть 4/7 от 7/9 .
Для того, чтобы найти дробь от числа, необходимо умножить число на эту дробь.
Значит, во второй день бригада отремонтировала
7/9•4/7=(7•4)/(9•7)=4/9 части пути.
Итак, после первого дня оставалось отремонтировать 7/9 части пути, во второй день отремонтировали 4/9 части пути.
Значит, в третий день осталось отремонтировать
7/9-4/9=(7-4)/9=3/9=(3•1)/(3•3)=1/3 часть всего пути, которым соответствуют 6 км.
Для того, чтобы найти число по данному значению его дроби, необходимо это значение разделить на дробь.
Тогда, длина всего пути
6:1/3=6•3/1=6•3=18 км.
Ответ: 18 км.
Запишите число, обратное числу:
a) 3/11; б) 6; в) 7 1/7; г) 0,25; д) 3,2.
Два числа, произведение которых равно 1, называются взаимно обратными.
При умножении двух дробей получим единицу, если числитель первой дроби равен знаменателю второй дроби, а знаменатель первой дроби равен числителю второй дроби.
Следовательно, чтобы получить дробь обратную данной, необходимо у данной дроби поменять местами числитель и знаменатель.
а) Дроби 3/11 обратной будет дробь 11/3 которая является неправильной, так как 11>3, значит, её можно преобразовать в смешанное число.
Для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, необходимо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток – как числитель его дробной части.
Тогда, 11/3=3 2/3 , так как 11:3=3 (ост.2).
Следовательно, числу 3/11 обратно число 3 2/3 .
б) 6=6/1 , так как дробь, у которой в знаменателе стоит 1, равна числителю.
Дроби 6/1 обратной будет дробь 1/6 , значит, и числу 6 обратным будет число 1/6 .
в) Для того, чтобы найти число обратное смешанному числу 7 1/7 , его необходимо преобразовать в неправильную дробь.
Для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа, получим
7 1/7=50/7 , так как 7•7+1=49+1=50 .
Дроби 50/7 обратной будет дробь 7/50 , значит, и числу 7 1/7 обратной будет дробь 7/50 .
г) Десятичную дробь всегда можно преобразовать в обыкновенную, у которой в знаменателе стоит единица с нулями (число нулей в знаменателе равно количеству цифр после запятой).
Значит, 0,25=25/100=(25•1)/(25•4)=1/4 , а дроби 1/4 обратной будет дробь 4/1, которая равна 4, так как дробь, у которой в знаменателе стоит 1, равна числителю.
Следовательно, числу 0,25 обратным будет число 4.
д) 3,2=3 2/10=3 (2•1)/(2•5)=3 1/5=16/5 , а дроби 16/5 обратной будет дробь 5/16.
Следовательно, числу 3,2 обратным будет число 5/16 .
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







