Упр.4.315 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)


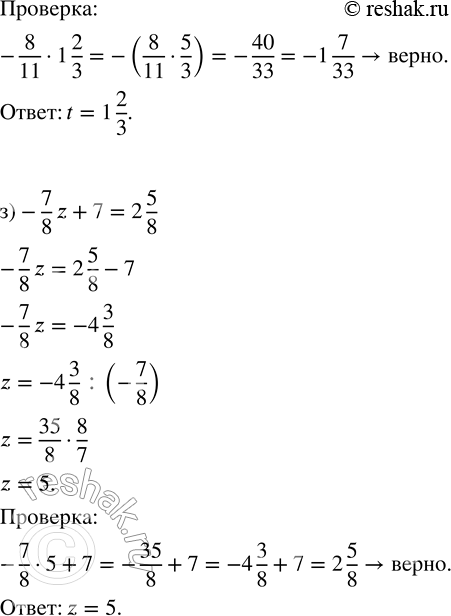
Решение #2 (Учебник 2023)






Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите корень уравнения и выполните проверку:
а) -z · 5 = -150; в) -0,4y = 44; д) 5/7 t = -25/28; ж) -8/11 t = -1 7/33;
б) 4 · (-z) = -32; г) 1/7 z = -1; е) -4/9 z = 16/27; з) -7/8 z + 7 = 2 5/8.
В каждом из данных уравнений неизвестен множитель.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель.
Числа x и -x противоположные, значит, и числа им соответствующие должны отличаться только знаками.
Для того, чтобы выполнить проверку, необходимо в уравнение подставить число, которое получилось после деления, и выполнить умножение, если левая и правая части выражения будут равны, то уравнение решено верно.
При выполнении вычислений опираемся на следующие правила:
- для того, чтобы сложить числа с разными знаками, необходимо найти модули слагаемых и из большего модуля вычесть меньший модуль; перед полученным числом поставить знак слагаемого с большим модулем.
- для того, чтобы перемножить два числа с разными знаками, необходимо умножить их модули и перед полученным произведением поставить знак «-».
- для того, чтобы найти частное двух отрицательных чисел, необходимо разделить модуль делимого на модуль делителя.
- для того, чтобы найти частное двух чисел с разными знаками, необходимо разделить модуль делимого на модуль делителя и поставить перед полученным числом знак «-».
- для того, чтобы разделить десятичную дробь на десятичную, необходимо перенести в делимом и делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе и выполнить деление на натуральное число, то есть разделить дробь на это число, не обращая внимание на запятую; поставить в частном запятую, когда кончится деление целой части.
- для того, чтобы разделить одну дробь на другую, необходимо делимое умножить на число, обратное делителю, то есть у делителя нужно поменять местами числа стоящие в числителе и знаменателе.
- для того, чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменения.
- для того, чтобы выполнить деление смешанных чисел, необходимо записать эти числа в виде неправильных дробей.
Для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
- произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
- для того, чтобы выполнить вычитание смешанных чисел, необходимо привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую часть; отдельно выполнить вычитание целых частей и отдельно дробных частей.
а) -z•5=-150
-z=-150:5
-z=-(150:5)
-z=-30
z=30
Проверка: -z•5=-30•5=-(30•5)=-150 - верно.
б) 4•(-z)=-32
-z=-32:4
-z=-(32:4)
-z=-8
z=8
Проверка: 4•(-z)=4•(-8)=-(4•8)=-32 - верно.
в) -0,4y=44
y=44:(-0,4)
y=-(44:0,4)
y=-(440:4)
y=-110
Проверка: -0,4y=-0,4•(-110)=0,4•110=44 - верно.
г) 1/7 z=-1
z=-1:1/7
z=-(1:1/7)
z=-(1•7)
z=-7
Проверка: 1/7 z=1/7•(-7)=-(1/7•7)=-(1•7)/7=-7/7=-1 - верно.
д) 5/7 t=-25/28
t=-25/28 :5/7
t=-(25/28 :5/7)
t=-(25/28•7/5)
t=-(25•7)/(28•5)
t=-(5•5•7)/(4•7•5)
t=-5/4
t=-1 1/4
Проверка:
5/7 t=5/7•(-1 1/4)=5/7•(-5/4)=-(5/7•5/4)=-(5•5)/(7•4)=-25/28 верно.
е) -4/9 z=16/27
z=16/27 :(-4/9)
z=-(16/27 :4/9)
z=-(16/27•9/4)
z=-(16•9)/(27•4)
z=-(4•4•9)/(3•9•4)
z=-4/3
z=-1 1/3
Проверка: -4/9 z=-4/9•(-1 1/3)=4/9•1 1/3=4/9•4/3=(4•4)/(9•3)=16/27 - верно.
ж) -8/11 t=-1 7/33
t=-1 7/33 :(-8/11)
t=1 7/33 :8/11
t=40/33 :8/11
t=40/33•11/8
t=(40•11)/(33•8)
t=(5•8•11)/(3•11•8)
t=1 2/3
Проверка:
-8/11 t=-8/11•1 2/3=-(8/11•5/3)=-(8•5)/(11•3)=-40/33=-1 7/33 - верно.
з) -7/8 z+7=2 5/8
Неизвестно слагаемое -7/8 z.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим
-7/8 z=2 5/8-7
-7/8 z=-(7-2 5/8)
-7/8 z=-(6 8/8-2 5/8)
-7/8 z=-((6-2)+(8/8-5/8))
-7/8 z=-(4+(8-5)/8)
-7/8 z=-4 3/8
z=-4 3/8 :(-7/8)
z=4 3/8 :7/8
z=35/8•8/7
z=(35•8)/(8•7)
z=35/7
z=5
Проверка:
-7/8 z+7=-7/8•5+7=-(7•5)/8+7=-35/8+7=-4 3/8+7=7-4 3/8=6 8/8-4 3/8=(6-4)+(8/8-3/8)=2+(8-3)/8=2 5/8 - верно.
При вычислениях, если возможно, выполняем сокращение.
Если при вычислениях получаем неправильную дробь, то преобразуем её в смешанное число.
Для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, необходимо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток – как числитель его дробной части.
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







