Упр.4.377 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)
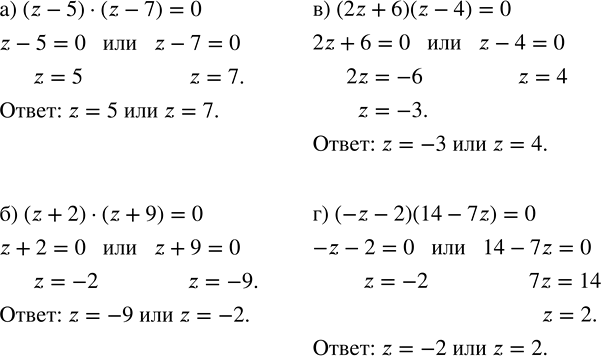
Решение #2 (Учебник 2023)


Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите корень уравнения:
а) (z - 5) · (z - 7) = 0; в) (2z + 6)(z - 4) = 0;
б) (z + 2) · (z + 9) = 0; г) (-z - 2)(14 - 7z) = 0.
Произведение равно нулю, если какой - либо из множителей или оба множителя равны нулю.
а) В уравнении (z-5)•(z-7)=0 нулю может быть равен либо первый множитель, либо второй, тогда
z-5=0 или z-7=0
В полученных уравнениях неизвестны уменьшаемые z.
Для того, чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое, получим
z=0+5 или z=0+7 или, выполнив сложение,
z=5 или z=7.
б) В уравнении (z+2)•(z+9)=0 нулю может быть равен либо первый множитель, либо второй, тогда
z+2=0 или z+9=0
В полученных уравнениях неизвестны слагаемые z.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим
z=0-2 или z=0-9 или, выполнив вычитание,
z=-2 или z=-9.
в) В уравнении (2z+6)•(z-4)=0 нулю может быть равен либо первый множитель, либо второй, тогда
2z+6=0 или z-4=0
В первом полученном уравнении неизвестно слагаемое 2z.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим 2z=0-6 или, выполнив сложение, 2z=-6.
В получившемся уравнении неизвестен множитель z.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
z=-6:2 или, выполнив деление, z=-3.
Во втором полученном уравнении неизвестно уменьшаемое z.
Для того, чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое, получим
z=0+4 или, выполнив сложение, z=4.
г) В уравнении (-z-2)•(14-7z)=0 нулю может быть равен либо первый множитель, либо второй, тогда
-z-2=0 или 14-7z=0
В первом полученном уравнении неизвестно уменьшаемое -z.
Для того, чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое, получим -z=0+2 или, выполнив сложение, -z=2, то есть z=-2.
Во втором полученном уравнении неизвестно вычитаемое 7z.
Для того, чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность, получим
7z=14-0 или, выполнив вычитание, 7z=14.
В получившемся уравнении неизвестен множитель z.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
z=14:7 или, выполнив деление, z=2.
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







