Упр.494 ГДЗ Колягин Ткачёва 7 класс (Алгебра)
Решение #1
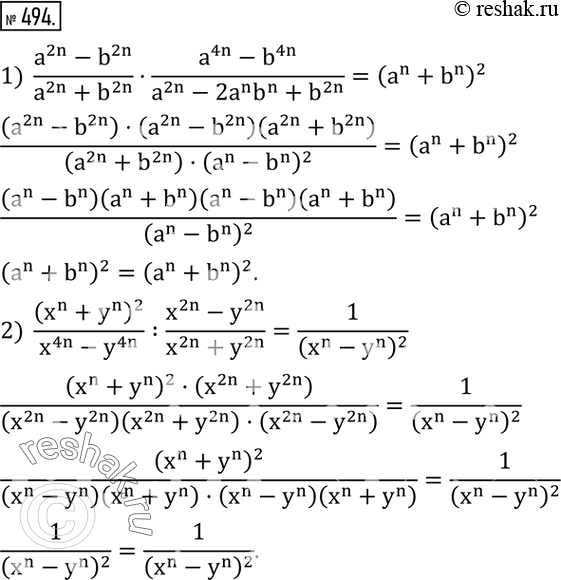

Рассмотрим вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 7 класс, Просвещение:
494. Доказать, что при всех допустимых значениях a, b, x и y (n - натуральное число) верно равенство:
1) (a^2n-b^2n)/(a^2n+b^2n )•(a^4n-b^4n)/(a^2n-2a^n b^n+b^2n )=(a^n+b^n )^2;
2) (x^n+y^n )^2/(x^4n-y^4n ) :(x^2n-y^2n)/(x^2n+y^2n )=1/(x^n-y^n )^2 .
Популярные решебники 7 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением





