Упр.5.100 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)
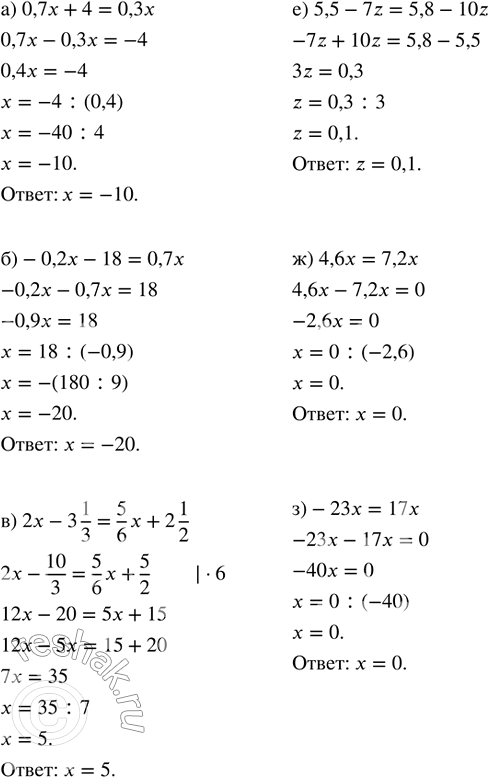
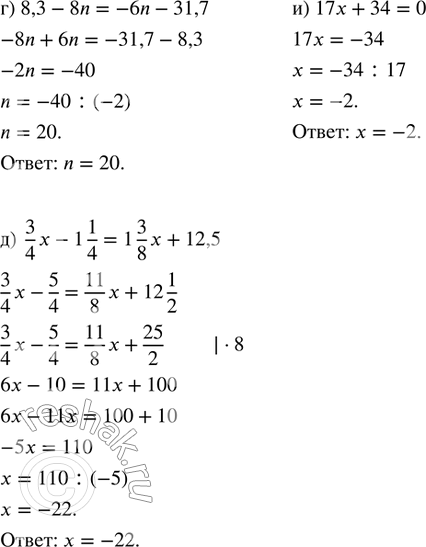
Решение #2 (Учебник 2023)






Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Решите уравнение:
а) 0,7x + 4 = 0,3x; г) 8,3 - 8n = -6n - 31,7; ж) 4,6x = 7,2x;
б) -0,2x - 18 = 0,7x; д) 3/4 x - 1 1/4 = 1 3/8 x + 12,5; з) -23x = 17x;
в) 2x - 3 1/3 = 5/6 x + 2 1/2; е) 5,5 - 7z = 5,8 - 10z; и) 17x + 34 = 0.
Известно, что корни уравнения не изменяются:
- если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак, то есть при переносе слагаемого из левой части в правую или наоборот, необходимо поменять его знак на противоположный.
- если обе части уравнения умножить или разделить на одно и то же число, не равное нулю.
Для решений данных уравнений соберём в левой части уравнения все слагаемые, содержащие неизвестное, а в правой – не содержащие неизвестное, затем приведём подобные слагаемые, то есть сложим их коэффициенты и полученный результат умножим на общую буквенную часть.
В том случае, если в уравнении есть коэффициенты – обыкновенные дроби или смешанные числа, сначала избавляемся от всех дробных коэффициентов, для этого умножим обе части уравнения на наименьший общий знаменатель дробей.
При этом помним, что:
- для того, чтобы сложить два числа с разными знаками, необходимо найти модули слагаемых и из большего модуля вычесть меньший; перед полученным числом поставить знак слагаемого с большим модулем.
- для того, чтобы сложить два отрицательных числа, необходимо найти и сложить модули слагаемых; перед полученным числом поставить знак «-».
- для того, чтобы из данного числа вычесть другое, необходимо к уменьшаемому прибавить число, противоположное вычитаемому.
Для того, чтобы найти частное двух отрицательных чисел, необходимо разделить модуль делимого на модуль делителя.
Для того, чтобы найти частное двух чисел с разными знаками, необходимо разделить модуль делимого на модуль делителя и поставить перед полученным числом знак «-».
а) 0,7x+4=0,3x
Второе слагаемое левой части переносим вправо, а слагаемое правой части – влево, при этом поменяв их знаки на противоположные, так как слагаемые положительны, то при переносе они будут иметь знак минус, получаем:
0,7x-0,3x=-4
0,4x=-4
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=-4:0,4
x=-40:4
x=-10
б) -0,2x-18=0,7x
-0,2x+(-18)=0,7x
Второе слагаемое левой части переносим вправо, а слагаемое правой части – влево, при этом поменяв их знаки на противоположные, так как слагаемое (-18) отрицательно, а слагаемое 0,7x положительно, то при переносе они будут иметь знаки плюс и минус соответственно, получаем:
-0,2x-0,7x=18
-(0,2+0,7)x=18
-0,9x=18
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=18:(-0,9)
x=-(180:9)
x=-20
в) 2x-3 1/3=5/6 x+2 1/2
Сначала переведём смешанные числа в неправильные дроби, для этого необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
2x-10/3=5/6 x+5/2
Теперь умножаем левую и правую части уравнения на 6 :
6•(2x-10/3)=6•(5/6 x+5/2) , получаем
12x-(6•10)/3=(6•5)/6 x+(6•5)/2
12x-(2•3•10)/3=(6•5)/6 x+(2•3•5)/2
12x-20=5x+15
Переносим в левую часть уравнения все слагаемые, которые содержат неизвестную, а в правую, которые не содержат:
12x-5x=20+15
7x=35
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=35:7
x=5
г) 8,3-8n=-6n-31,7
Первое слагаемое левой части переносим вправо, а первое слагаемое правой части – влево, при этом поменяв их знаки на противоположные, так как слагаемое 8,3 положительно, а слагаемое -6n отрицательно, то при переносе они будут иметь знаки минус и плюс соответственно, получаем:
-8n+6n=-8,3-31,7
-(8n-6n)=-(8,3+31,7)
-2n=-40
В полученном уравнении неизвестен множитель n.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
n=-40:(-2)
n=20
д) 3/4 x-1 1/4=1 3/8 x+12,5
3/4 x-1 1/4=1 3/8 x+12 5/10
3/4 x-1 1/4=1 3/8 x+12 5/(2•5)
3/4 x-1 1/4=1 3/8 x+12 1/2
Сначала переведём смешанные числа в неправильные дроби, для этого необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
3/4 x-5/4=11/8 x+25/2
Теперь умножаем левую и правую части уравнения на 8 :
8•(3/4 x-5/4)=8•(11/8 x+25/2) , получаем
(8•3)/4 x-(8•5)/4=(8•11)/8 x+(8•25)/2
(2•4•3)/4 x-(2•4•5)/4=(8•11)/8 x+(2•4•25)/2
6x-10=11x+100
Переносим в левую часть уравнения все слагаемые, которые содержат неизвестную, а в правую, которые не содержат:
6x-11x=10+100
-(11x-6x)=110
-5x=110
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=110:(-5)
x=-22
е) 5,5-7z=5,8-10z
Первое слагаемое левой части переносим вправо, а второе слагаемое правой части – влево, при этом поменяв их знаки на противоположные, так как слагаемое 5,5 положительно, а слагаемое -10z отрицательно, то при переносе они будут иметь знаки минус и плюс соответственно, получаем:
-7z+10z=-5,5+5,8
10z-7z=5,8-5,5
3z=0,3
В полученном уравнении неизвестен множитель z.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
z=0,3:3
z=0,1
ж) 4,6x=7,2x
Слагаемое правой части переносим влево, при этом поменяв его знак на противоположный, так как слагаемое 7,2x положительно, то при переносе оно будет иметь знак минус, получаем:
4,6x-7,2x=0
-(7,2x-4,6x)=0
-2,6x=0
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=0:(-2,6)
x=0
з) -23x=17x
Слагаемое правой части переносим влево, при этом поменяв его знак на противоположный, так как слагаемое 17x положительно, то при переносе оно будет иметь знак минус, получаем:
-23x-17x=0
-(23x+17x)=0
-40x=0
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=0:(-40)
x=0
и) 17x+34=0
Второе слагаемое левой части переносим вправо, при этом поменяв его знак на противоположный, так как слагаемое 34 положительно, то при переносе он будет иметь знак минус, получаем:
17x=-34
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=-34:17
x=-2
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







