Упр.5.373 ГДЗ Виленкин Жохов 5 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)
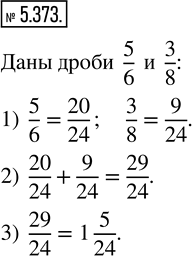
Решение #2 (Учебник 2023)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Александрова 5 класс, Просвещение:
Выполните действия по алгоритму:
1) Приведите дроби 5/6 и 3/8 к общему знаменателю.
2) Сложите полученные дроби с одинаковыми знаменателями.
3) Выделите целую часть дроби.
1) Наименьший общий знаменатель дробей - 24.
5/6=(5•4)/(6•4)=20/24
3/8=(3•3)/(8•3)=9/24
2) 20/24+9/24=(20+9)/24=29/24
3) Если при сложении получается неправильная дробь, то выделяем из этой неправильной дроби целую часть.
Для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, то есть выделить целую часть, необходимо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток – как числитель дробной части.
При выделении целой части из неправильной дроби 29/24 используем то, что 29:24=1 (ост.5).
29/24=1 5/24
Популярные решебники 5 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







