Упр.5.43 ГДЗ Погорелов 7-9 класс (Геометрия)
Решение #1
Рассмотрим вариант решения задания из учебника Погорелов 7 класс, Просвещение:
43. Докажите, что: 1) около любого треугольника можно описать окружность, и только одну; 2) в любой треугольник можно вписать окружность, и только одну.
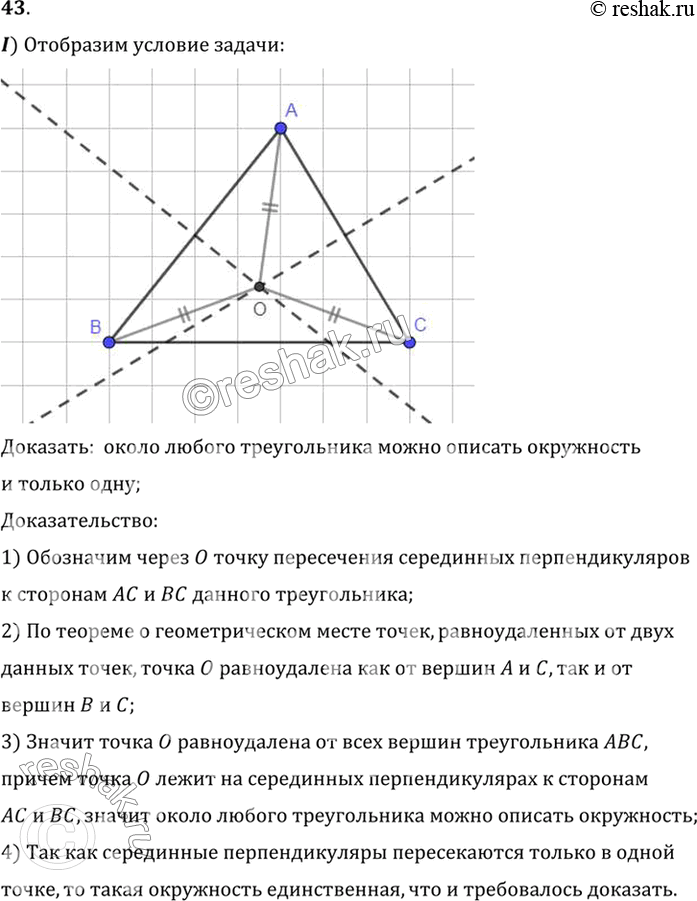
I) Отобразим условие задачи:
Доказать: около любого треугольника можно описать окружность
и только одну;
Доказательство:
1) Обозначим через O точку пересечения серединных перпендикуляров
к сторонам AC и BC данного треугольника;
2) По теореме о геометрическом месте точек, равноудаленных от двух
данных точек, точка O равноудалена как от вершин A и C, так и от
вершин B и C;
3) Значит точка O равноудалена от всех вершин треугольника ABC,
причем точка O лежит на серединных перпендикулярах к сторонам
AC и BC, значит около любого треугольника можно описать окружность;
4) Так как серединные перпендикуляры пересекаются только в одной
точке, то такая окружность единственная, что и требовалось доказать.
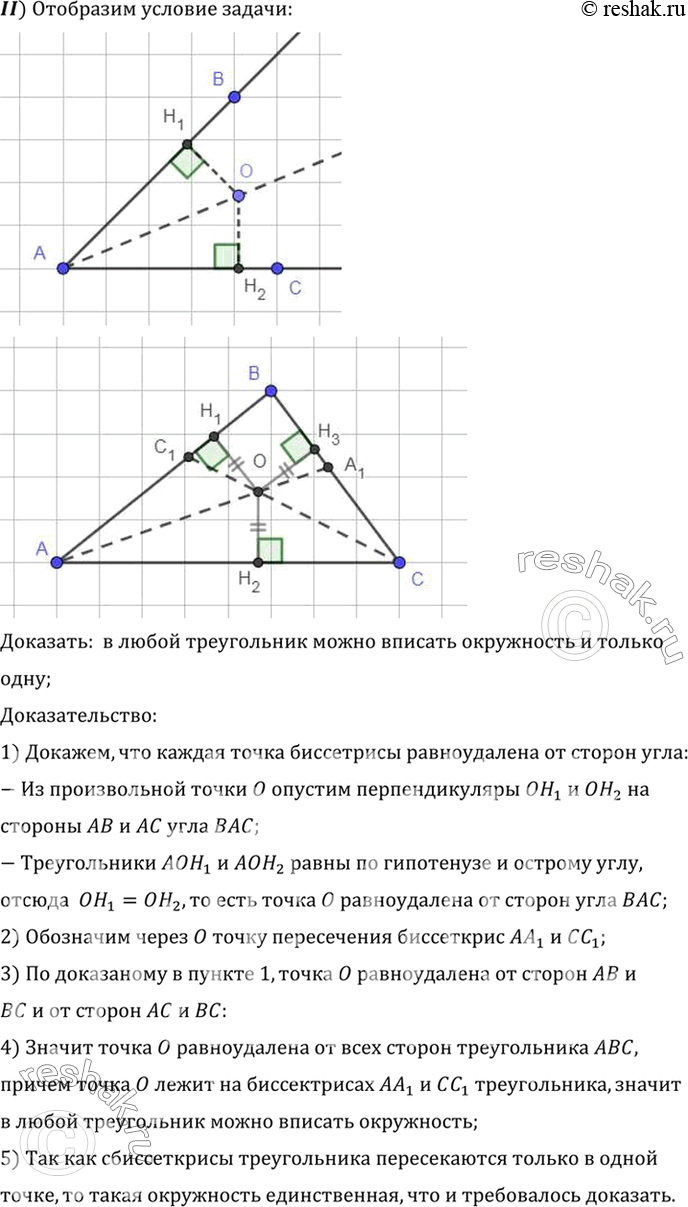
II) Отобразим условие задачи:
Доказать: в любой треугольник можно вписать окружность и только
одну;
Доказательство:
1) Докажем, что каждая точка биссетрисы равноудалена от сторон угла:
- Из произвольной точки O опустим перпендикуляры OH1 и OH2 на
стороны AB и AC угла BAC;
- Треугольники AOH1 и AOH2 равны по гипотенузе и острому углу,
отсюда OH1=OH2, то есть точка O равноудалена от сторон угла BAC;
2) Обозначим через O точку пересечения биссеткрис AA1 и CC1;
3) По доказаному в пункте 1, точка O равноудалена от сторон AB и
BC и от сторон AC и BC:
4) Значит точка O равноудалена от всех сторон треугольника ABC,
причем точка O лежит на биссектрисах AA1 и CC1 треугольника, значит
в любой треугольник можно вписать окружность;
5) Так как сбиссеткрисы треугольника пересекаются только в одной
точке, то такая окружность единственная, что и требовалось доказать.
Популярные решебники 7 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением





