Упр.5.72 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)
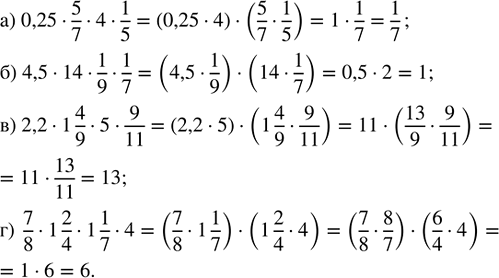
Решение #2 (Учебник 2023)


Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите произведение:
а) 0,25 · 5/7 · 4 · 1/5; б) 4,5 · 14 · 1/9 · 1/7; в) 2,2 · 1 4/9 · 5 · 9/11; г) 7/8 · 1 2/4 · 1 1/7 · 4.
Опираясь на переместительное и сочетательное свойства умножения, в произведении нескольких чисел множители можно менять местами, расставлять и раскрывать скобки, тем самым определяя наиболее удобный порядок выполнения действий.
При выполнении вычислений опираемся на следующие правила:
- для того, чтобы умножить десятичную дробь на натуральное число, необходимо умножить их как натуральные числа, не обращая внимание на запятую; в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятой у умножаемой дроби.
- для того, чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменения.
- произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
- для того, чтобы выполнить умножение смешанных чисел, необходимо записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
- произведение взаимно обратных чисел (чисел, у которых числитель и знаменатель поменяли местами) равно единице.
При выполнении умножения обыкновенных дробей, если возможно, выполняем сокращение.
Также учитываем то, что черту дроби можно заменить делением (числитель делим на знаменатель, если возможно).
а) 0,25•5/7•4•1/5=(0,25•4)•(5/7•1/5)=1•5/(7•5)=1/7
б) 4,5•14•1/9•1/7=(4,5•1/9)•(14•1/7)=(45/10•1/9)•14/7=(5•9)/(5•2•9)•(2•7)/7=1/2•2/1=1
в) 2,2•1 4/9•5•9/11=22/10•13/9•5•9/11=(22•13•5•9)/(10•9•11)=(2•11•13•5•9)/(2•5•9•11)=13/1=13
г) 7/8•1 2/4•1 1/7•4=7/8•6/4•8/7•4=(7•6•8•4)/(8•4•7)=6/1=6
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







