Упр.2.113 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
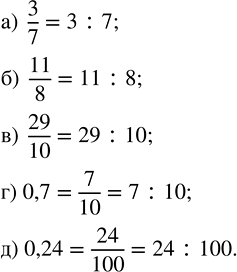
Решение #2 (Учебник 2023)


Решение #3 (Учебник 2021)

Решение #4 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Запишите в виде частного дробь:
а) 3/7; б) 11/8; в) 29/10; г) 0,7; д) 0,24.
Черту обыкновенной дроби можно понимать как знак деления, то есть a/b=a:b
а) 3/7=3:7
Числитель 3 является делимым.
Знаменатель 7 является делителем.
б) 11/8=11:8
Числитель 11 является делимым.
Знаменатель 8 является делителем.
в) 29/10=29:10
Числитель 29 является делимым.
Знаменатель 10 является делителем.
г) При переводе десятичной дроби (0,7) в обыкновенную в числителе дроби записывают число, стоящее после запятой (число 7), а разрядная единица в знаменателе содержит один ноль (столько знаков после запятой в десятичной дроби).
0,7=7/10
Тогда, решение будет записано так,
0,7=7/10=7:10
д) При переводе десятичной дроби (0,24) в обыкновенную в числителе дроби записывают число, стоящее после запятой (число 24), а разрядная единица в знаменателе содержит два нуля (столько знаков после запятой в десятичной дроби).
0,24=24/100
Тогда, решение будет записано так,
0,24=24/100=24:100
Докажите, что если число у кратно 14, то оно делится на 7.
Число y кратно 14 (число y делится на 14).
Это значит, что y можно представить в виде произведения
y=14•a
Число a – некоторое целое число.
Число 14 можно тоже представить в виде произведения множителей 2 и 7 (делители числа 14).
14=2•7
Или y=2•7•a
Выясним, можно ли произведение 2•7•a разделить на 7.
(2•7•a) :7= ?
Для того, чтобы произведение 2•7•a разделить на число 7, можно разделить на 7 только один из множителей и полученное частное умножить на остальные сомножители.
(2•7•a) :7=(7:7)•2•a=1•2•a=2a
Таким образом, деление выполнимо, то есть число y делится на 7.
Что и требовалось доказать.
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







