Упр.2.127 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)

Решение #3 (Учебник 2021)
Решение #4 (Учебник 2021)



Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Выполните действия:
а) (854,9 - 203,3) : 7,2 · 1,4 + 3,3; б) (150,4 + 87,5) : 7,8 · 2,5 - 4,5.
Если в выражении есть скобки, то сначала выполняют действия в скобках.
Если выражение содержит действия первой и второй ступени, то сначала выполняют действия второй ступени по порядку слева направо, а потом действия первой ступени, также по порядку слева направо.
При этом сложение и вычитание чисел называют действиями первой ступени, а умножение и деление чисел – действиями второй ступени.
Над примерами расставим цифрами порядок действий.
а) (854,9-203,3) :7,2•1,4+3,3=651,6:7,2•1,4+3,3=90,5•1,4+3,3=126,7+3,3=130
б) (150,4+87,5) :7,8•2,5-4,5=237,9:7,8•2,5-4,5=30,5•2,5-4,5=76,25-4,5=71,75
Найдите корень уравнения:
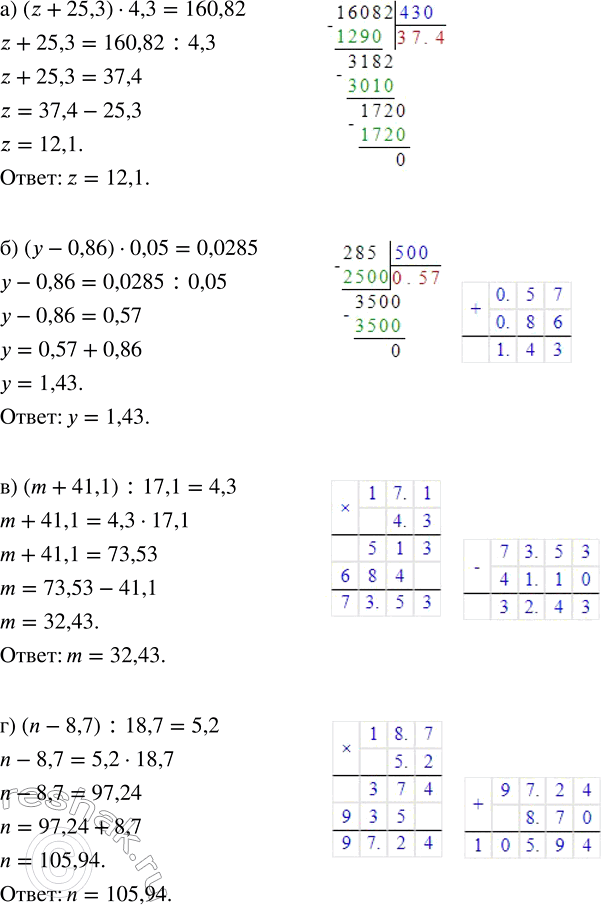
а) (z + 25,3) · 4,3 = 160,82; в) (m + 41,1) : 17,1 = 4,3;
б) (у - 0,86) · 0,05 = 0,0285; г) (n - 8,7) : 18,7 = 5,2.
а) (z+25,3)•4,3=160,82
Решим уравнение относительно умножения, то есть неизвестен множитель z+25,3.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
z+25,3=160,82:4,3
Или, выполнив деление,
z+25,3=37,4
Теперь решаем уравнение относительно сложения, то есть неизвестен множитель z.
Для того, чтобы найти неизвестный множитель, необходимо из суммы вычесть известный множитель, получим
z=37,4-25,3
Или, выполнив вычитание,
z=12,1
б) (y-0,86)•0,05=0,0285
Решим уравнение относительно умножения, то есть неизвестен множитель y-0,86.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
y-0,86=0,0285:0,05
Или, выполнив деление,
y-0,86=0,57
Теперь решаем уравнение относительно вычитания, то есть неизвестно уменьшаемое y.
Для того, чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое, получим
y=0,57+0,86
Или, выполнив сложение,
y=1,43
в) (m+41,1) :17,1=4,3
Решим уравнение относительно деления, то есть неизвестно делимое m+41,1.
Для того, чтобы найти неизвестное делимое, необходимо частное умножить на делитель, получим
m+41,1=4,3•17,1
Или, выполнив умножение,
m+41,1=73,53
Теперь решаем уравнение относительно сложения, то есть неизвестно слагаемое m.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим
m=73,53-41,1
Или, выполнив вычитание,
m=32,43
г) (n-8,7) :18,7=5,2
Решим уравнение относительно деления, то есть неизвестно делимое n-8,7.
Для того, чтобы найти неизвестное делимое, необходимо частное умножить на делитель, получим
n-8,7=5,2•18,7
Или, выполнив умножение,
n-8,7=97,24
Теперь решаем уравнение относительно вычитания, то есть неизвестно уменьшаемое m.
Для того, чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое, получим
n=97,24+8,7
Или, выполнив сложение,
n=105,94
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







