Упр.2.164 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
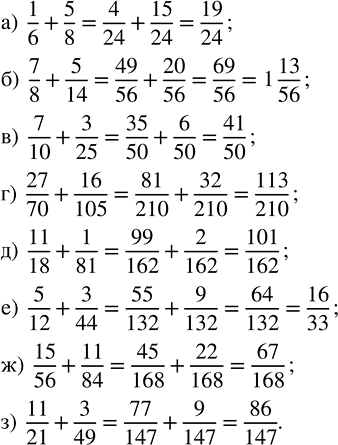
Решение #2 (Учебник 2023)
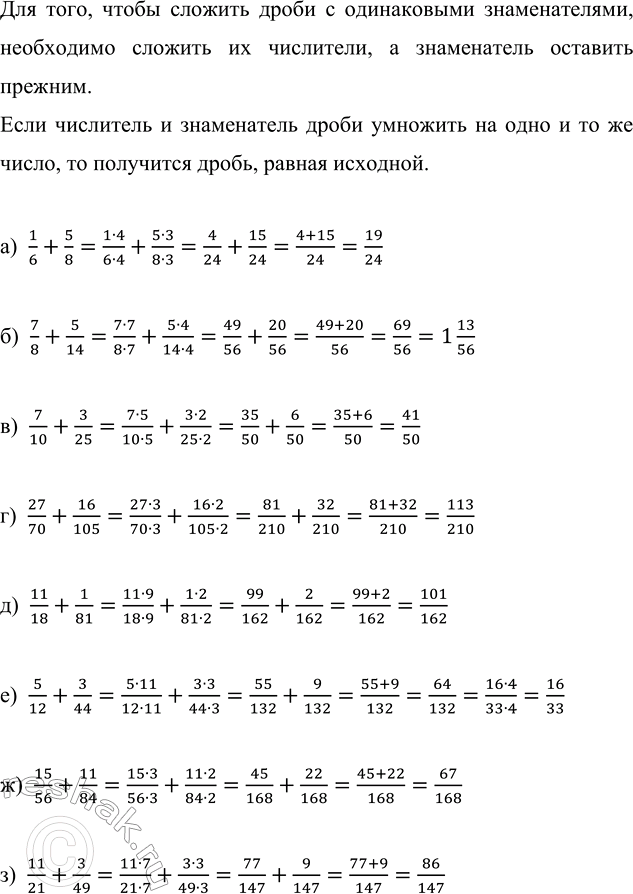
Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)

Решение #5 (Учебник 2021)


Решение #6 (Учебник 2021)
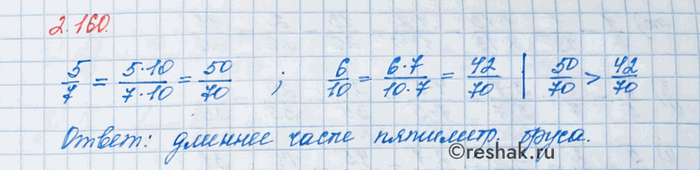
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите сумму:
а) 1/6 + 5/8; в) 7/10 + 3/25; д) 11/18 + 1/81; ж) 15/56 + 11/84;
б) 7/8 + 5/14; г) 27/70 + 16/105; е) 5/12 + 3/44; з) 11/21 + 3/49.
Для того, чтобы сложить дроби с одинаковыми знаменателями, необходимо сложить их числители, а знаменатель оставить прежним.
Если числитель и знаменатель дроби умножить на одно и то же число, то получится дробь, равная исходной.
а) 1/6+5/8=(1•4)/(6•4)+(5•3)/(8•3)=4/24+15/24=(4+15)/24=19/24
б) 7/8+5/14=(7•7)/(8•7)+(5•4)/(14•4)=49/56+20/56=(49+20)/56=69/56=1 13/56
в) 7/10+3/25=(7•5)/(10•5)+(3•2)/(25•2)=35/50+6/50=(35+6)/50=41/50
г) 27/70+16/105=(27•3)/(70•3)+(16•2)/(105•2)=81/210+32/210=(81+32)/210=113/210
д) 11/18+1/81=(11•9)/(18•9)+(1•2)/(81•2)=99/162+2/162=(99+2)/162=101/162
е) 5/12+3/44=(5•11)/(12•11)+(3•3)/(44•3)=55/132+9/132=(55+9)/132=64/132=(16•4)/(33•4)=16/33
ж) 15/56+11/84=(15•3)/(56•3)+(11•2)/(84•2)=45/168+22/168=(45+22)/168=67/168
з) 11/21+3/49=(11•7)/(21•7)+(3•3)/(49•3)=77/147+9/147=(77+9)/147=86/147
Части какого бруса длиннее: пятиметрового, распиленного на 7 равных частей, или шестиметрового, распиленного на 10 равных частей?
Для того, чтобы определить длину одной части пятиметрового бревна после распиливания бревна на семь частей, необходимо 5 м разделить на 7.
5 м:7=5/7 м.
После распиливания длина одной части пятиметрового бревна равна 5/7 м.
Для того, чтобы определить длину одной части шестиметрового бревна после распиливания бревна на десять частей, необходимо 6 м разделить на 10.
6 м:10=6/10 м.
После распиливания длина одной части шестиметрового бревна равна 6/10 м.
Для того, чтобы выяснить, части какого бревна длиннее, необходимо сравнить 5/7 м и 6/10 м.
То есть сравнить дроби 5/7 и 6/10 .
Для того, чтобы сравнить дроби 5/7 и 6/10 , необходимо привести их к общему знаменателю.
Для того, чтобы привести дроби 5/7 и 6/10 к общему знаменателю, необходимо определить их наименьший общий знаменатель (или наименьшее общее кратное).
7 – простое число.
10=2•5
Для того, чтобы определить НОК, необходимо недостающие множители добавить к множителям большего числа и перемножить их:
НОК(7,10)=2•5•7=10•7=70
Далее определим дополнительные множители для дробей 5/7 и 6/10 .
70:7=10 – дополнительный множитель для дроби 5/7 .
5/7=(5•10)/(7•10)=50/70
70:10=7 – дополнительный множитель для дроби 6/10 .
6/10=(6•7)/(10•7)=42/70
Теперь сравниваем дроби 50/70 и 42/70 .
Так как 50>42, значит, 50/70>42/70
Таким образом, 5/7>6/10 .
Значит, части пятиметрового бревна (каждая по 5/7 м) длиннее, чем части шестиметрового бревна (каждая по 6/10 м).
Ответ: части пятиметрового бревна.
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







