Упр.2.181 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)


Решение #3 (Учебник 2023)
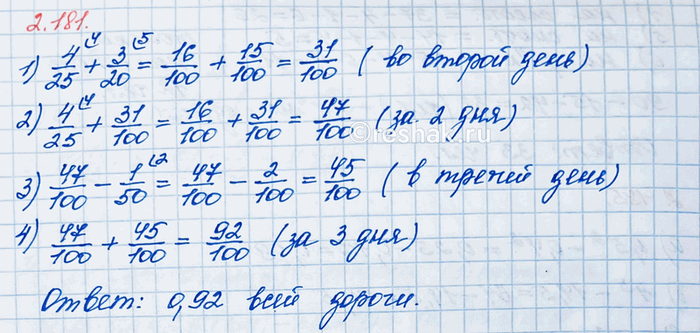
Решение #4 (Учебник 2021)

Решение #5 (Учебник 2021)

Решение #6 (Учебник 2021)
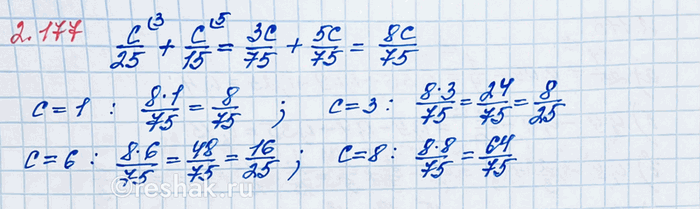
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
В первый день дорожно-строительной бригадой было отремонтировано 4/25 всей дороги, во второй день — на 3/20 больше, чем в первый, а в третий день — на 1/50 меньше, чем за два предыдущих дня вместе. Какую часть дороги отремонтировала бригада за три дня?
Для того, чтобы определить, какую часть дороги отремонтировали за 2 дня, необходимо сложить части дороги первого и второго дня.
Во второй день отремонтировали дороги больше, чем в первый.
Значит, найдём часть отремонтированной во второй день дороги, с помощью сложения.
При сложении (вычитании) дробей с одинаковыми знаменателями, их числители складывают (вычитают), а знаменатель оставляют тот же.
При умножении числителя и знаменателя дроби на одно и то же число, получается дробь равная данной.
4/25+3/20=(4•4)/(25•4)+(3•5)/(20•5)=16/100+15/100=(16+15)/100=31/100 (части) – дороги отремонтировали во второй день.
Теперь определим какую часть дороги отремонтировали за два первых дня.
4/25+31/100=(4•4)/(25•4)+31/100=16/100+31/100=(16+31)/100=47/100 (части) – дороги отремонтировали за два дня.
Известно, что в третий день отремонтировали дороги меньше, чем за два первых дня ремонта вместе.
Значит, найдём эту часть дороги с помощью вычитания.
47/100-1/50=47/100-(1•2)/(50•2)=47/100-2/100=(47-2)/100=45/100 (части) – дороги отремонтировали в третий день.
Наконец найдём, какую часть дороги отремонтировала бригада за три дня.
Для этого сложим часть дороги, отремонтированную за первые два дня, и часть дороги, отремонтированную в третий день.
47/100+45/100=(47+45)/100=92/100=0,92 (части) – дороги, которую отремонтировал бригада за 3 дня.
Ответ: 0,92 части.
Вычислите значение выражения c/25 + c/15 при с = 1; с = 3; с = 6; с = 8.
Упростим исходное выражение.
Для этого сложим дроби, приведя их к общему знаменателю 75.
При умножении числителя и знаменателя дроби на одно и то же число, получается дробь равная данной.
При сложении дробей с одинаковыми знаменателями, числители складывают, а знаменатель оставляют тот же.
c/25+c/15=(c•3)/(25•3)+(c•5)/(15•5)=3c/75+5c/75=(3c+5c)/75=8c/75
Подставим значения c в полученное выражение, и вычислим результат.
При c=1, получим 8c/75=(8•1)/75=8/75
При c=3, получим 8c/75=(8•3)/75=24/75=(3•8)/(3•25)=8/25
При c=6, получим 8c/75=(8•6)/75=48/75=(3•16)/(3•25)=16/25
При c=8, получим 8c/75=(8•8)/75=64/75
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







