Упр.2.180 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
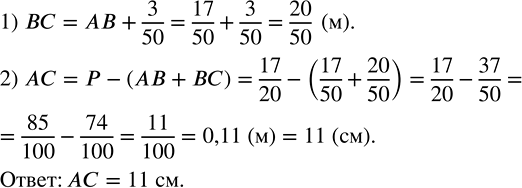
Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)
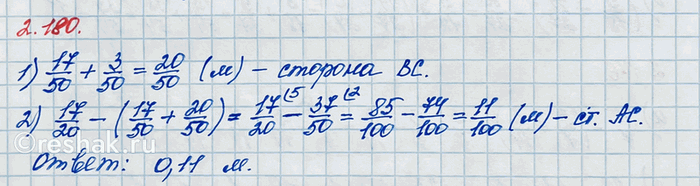
Решение #4 (Учебник 2021)
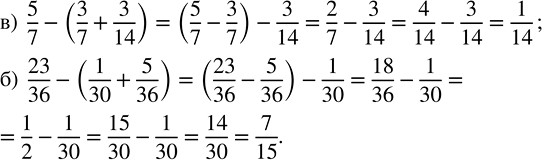
Решение #5 (Учебник 2021)

Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Периметр треугольника АВС равен 17/20 м. Сторона AВ равна 17/50 м, сторона ВС на 3/50 м длиннее AВ. Найдите сторону AС.
При умножении числителя и знаменателя дроби на одно и то же число, получается дробь равная данной.
При сложении дробей с одинаковыми знаменателями, их числители складывают, а знаменатель оставляют тот же.
Сторона АВ известна (17/50 м), а сторона ВС на 3/50 м длиннее, то есть больше, стороны АВ.
Значит, сторона ВС составляет:
17/50+3/50=(17+3)/50=20/50 (м) – сторона ВС.
Периметр треугольника равен сумме всех его сторон.
Так как две стороны треугольника известны, то для того, чтобы найти длину третьей стороны, необходимо из периметра треугольника вычесть сумму длин двух известных сторон.
По условию задачи, периметр треугольника АВС равен 17/20 м.
Тогда, длина стороны АС равна:
AC=P-(AB+BC)=17/20-(17/50+20/50)=17/20-(17+20)/50=17/20-37/50=
=(17•5)/(20•5)-(37•2)/(50•2)=85/100-74/100=(85-74)/100=11/100 (м)=0,11 (м)=11 (см) – длина стороны АС.
Ответ: 11 см.
С помощью свойства вычитания суммы из числа вычислите значение выражения:
а) 5/7 - (3/7 + 3/14); б) 23/36 - (1/30 + 5/36).
При сложении (вычитании) дробей с одинаковыми знаменателями, числители складывают (вычитают), а знаменатель оставляют тот же.
а) Для того, чтобы вычесть сумму 3/7+3/14 из дроби 5/7 , можно сначала вычесть из 5/7 слагаемое 3/7 с таким же знаменателем (7), и из полученной разности затем вычесть другое слагаемое 3/14 .
5/7-(3/7+3/14)=(5/7-3/7)-3/14=(5-3)/7-3/14=2/7-3/14
Приведём дроби к общему знаменателю 14.
2/7-3/14=(2•2)/(7•2)-3/14=4/14-3/14=(4-3)/14=1/14
б) Для того, чтобы вычесть сумму 1/30+5/36 из дроби 23/36 , можно сначала вычесть из 23/36 слагаемое 5/36 с таким же знаменателем (36), и из полученной разности затем вычесть другое слагаемое 1/30 .
23/36-(1/30+5/36)=(23/36-5/36)-1/30=(23-5)/36-1/30=18/36-1/30
Сократим первую дробь на 18.
18/36-1/30=(18•1)/(18•2)-1/30=1/2-1/30
Приведём дроби к общему знаменателю 30.
1/2-1/30=(1•15)/(2•15)-1/30=15/30-1/30=(15-1)/30=14/30
Сократим дробь на 2.
14/30=(2•7)/(2•15)=7/15
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







