Упр.2.245 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)
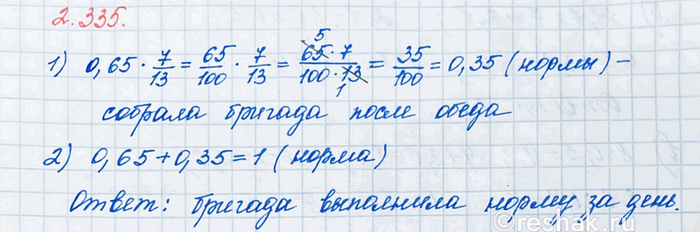
Решение #4 (Учебник 2021)
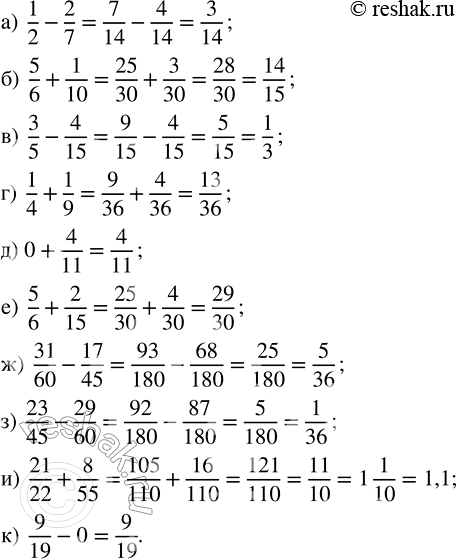
Решение #5 (Учебник 2021)


Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
До обеда бригада собрала 0,65 нормы хлопка, а после обеда — 7/13 нормы хлопка, собранного до обеда. Собрала ли бригада за день положенную норму хлопка?
Десятичную дробь 0,65 можно представить в виде обыкновенной дроби, у которой в знаменателе стоит единица с нулями (число нулей в знаменателе равно числу цифр после запятой у десятичной дроби).
Значит, 0,65=65/100 или, выполнив сокращение,
0,65=65/100=(5•13)/(5•20)=13/20 .
Для того, чтобы найти часть от числа, выраженную дробью, необходимо умножить число на эту дробь.
До обеда бригада собрала 0,65 нормы хлопка, а после обеда - 7/13 нормы хлопка, собранного до обеда.
Значит, после обеда бригада собрала
0,65•7/13=13/20•7/13=(13•7)/(20•13)=7/20 – нормы хлопка.
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей.
До обеда бригада собрала 0,65 нормы хлопка, после обеда - 7/20 нормы хлопка, значит, за весь день бригада собрала
0,65+7/20=13/20+7/20=(13+7)/20=20/20=1
Дробь, у которой числитель и знаменатель одинаковые, равна единице (целому), значит, бригада собрала за день положенную норму хлопка.
При сложении дробей с одинаковыми знаменателями, их числители складывают, а знаменатель оставляют тот же.
Ответ: Да, собрала.
Вычислите:
а) 1/2 - 2/7; в) 3/5 - 4/15; д) 0 + 4/11; ж) 31/60 - 17/45; и) 21/22 + 8/55;
б) 5/6 + 1/10; г) 1/4 + 1/9; е) 5/6 + 2/15; з) 23/45 - 29/60; к) 9/19 - 0.
При сложении (вычитании) дробей с одинаковыми знаменателями, их числители складывают (вычитают), а знаменатель оставляют тот же.
Если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится дробь равная данной.
Если в ответе получается сократимая дробь, необходимо числитель и знаменатель разделить на одно и то же число.
Если при вычислениях получается неправильная дробь, то есть дробь, у которой числитель больше знаменателя, то необходимо числитель разделить на знаменатель с остатком, далее целое записать в целую часть смешанного числа, остаток записать в числитель дроби, а знаменатель оставить тот же.
а) 1/2-2/7=(1•7)/(2•7)-(2•2)/(7•2)=7/14-4/14=(7-4)/14=3/14
б) 5/6+1/10=(5•5)/(6•5)+(1•3)/(10•3)=25/30+3/30=(25+3)/30=28/30=(2•14)/(2•15)=14/15
в) 3/5-4/15=(3•3)/(5•3)-4/15=9/15-4/15=(9-4)/15=5/15=(5•1)/(5•3)=1/3
г) 1/4+1/9=(1•9)/(4•9)+(1•4)/(9•4)=9/36+4/36=(9+4)/36=13/36
д) 0+4/11=4/11
е) 5/6+2/15=(5•5)/(6•5)+(2•2)/(15•2)=25/30+4/30=(25+4)/30=29/30
ж) 31/60-17/45=(31•3)/(60•3)-(17•4)/(45•4)=93/180-68/180=(93-68)/180=25/180=(5•5)/(5•36)=5/36
з) 23/45-29/60=(23•4)/(45•4)-(29•3)/(60•3)=92/180-87/180=(92-87)/180=5/180=(5•1)/(5•36)=1/36
и) 21/22+8/55=(21•5)/(22•5)+(8•2)/(55•2)=105/110+16/110=(105+16)/110=121/110=(11•11)/(11•10)=11/10=1 1/10
к) 9/19-0=9/19
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







