Упр.2.254 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
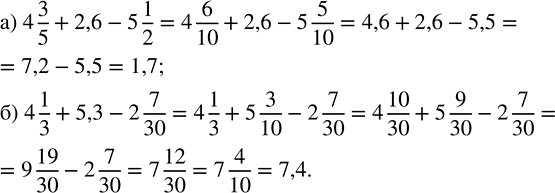
Решение #2 (Учебник 2023)


Решение #3 (Учебник 2023)
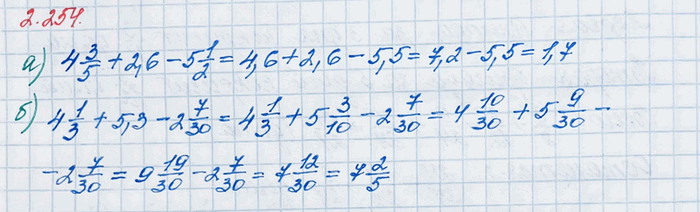
Решение #4 (Учебник 2021)
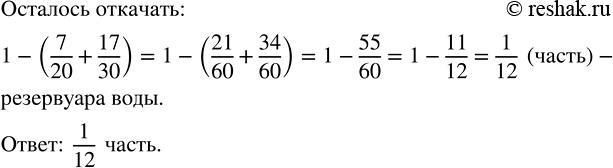
Решение #5 (Учебник 2021)

Решение #6 (Учебник 2021)
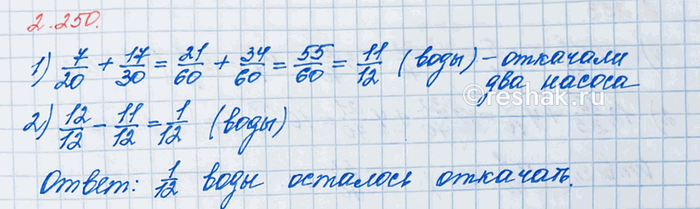
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Вычислите:
а) 4 3/5 + 2,6 - 5 1/2; б) 4 1/3 + 5,3 - 2 7/30.
Для того, чтобы выполнить сложение (вычитание) смешанных чисел, необходимо дробные части привести к общему знаменателю, затем отдельно выполнить сложение (вычитание) целых частей и дробных частей.
При умножении числителя и знаменателя дроби на одно и то же число, получается дробь равная данной.
Если в ответе получается сократимая дробь, необходимо числитель и знаменатель разделить на одно и то же число.
а) 4 3/5+2,6-5 1/2
Переведём обыкновенные дроби в десятичные.
Для того, чтобы дробь 4 3/5 представить в виде десятичной дроби, сначала расширяем эту дробь на число 2 (дополнительный множитель), чтобы в знаменателе получилась разрядная единица 10.
4 3/5=4 (3•2)/(5•2)=4 6/10
Для того, чтобы получившуюся дробь записать в виде десятичной дроби, сначала пишем целую часть, а потом числитель дробной части (4,6).
Для того, чтобы дробь 5 1/2 представить в виде десятичной дроби, сначала расширяем эту дробь на число 5 (дополнительный множитель), чтобы в знаменателе получилась разрядная единица 10.
5 1/2=5 (1•5)/(2•5)=5 5/10
Для того, чтобы получившуюся дробь записать в виде десятичной дроби, сначала пишем целую часть, а потом числитель дробной части (5,5).
4 3/5+2,6-5 1/2=4,6+2,6-5,5=7,2-5,5=1,7
б) 4 1/3+5,3-2 7/30
Обыкновенную дробь 1/3 нельзя перевести в десятичную (невозможно подобрать дополнительный множитель, чтобы привести дробь к новому знаменателю 10, 100, 1000 и так далее).
Поэтому переведём десятичную дробь 5,3 в обыкновенную дробь.
Для того, чтобы 5,3 перевести в обыкновенную дробь, в числителе дроби записываем число, стоящее после запятой (3), а в знаменателе 1 и столько же нулей, сколько знаков после запятой в десятичной дроби 5,3 (один знак), получим
5,3=5 3/10
4 1/3+5,3-2 7/30=4 1/3+5 3/10-2 7/30=4 (1•10)/(3•10)+5 (3•3)/(10•3)-2 7/30=4 10/30+5 9/30-2 7/30=(4+5-2)+(10/30+9/30-7/30)=7+(10+9-7)/30==7 12/30=7 (3•4)/(3•10)=7,4
Один насос откачал 7/20 резервуара воды, а другой — 17/30 этого же резервуара. Какую часть резервуара воды осталось откачать?
Для того, чтобы выполнить сложение (вычитание) смешанных чисел, необходимо дробные части привести к общему знаменателю, затем отдельно выполнить сложение (вычитание) целых частей и дробных частей.
При умножении числителя и знаменателя дроби на одно и то же число, получается дробь равная данной.
Когда на первом месте стоит целое число и из него необходимо вычесть смешанное число, нужно целое число представить в виде смешанного числа, у которого дробная часть будет являться неправильной дробью.
Если в ответе получается сократимая дробь, необходимо числитель и знаменатель разделить на одно и то же число.
Для того, чтобы найти, какую часть резервуара воды осталось откачать, необходимо из всего резервуара вычесть ту часть, которую откачали.
При этом в таких задачах принято общее обозначать за единицу.
Поэтому, резервуар воды – это единица, и из неё вычитаем то, что откачали оба насоса.
Тогда, 7/20+17/30=(7•3)/(20•3)+(17•2)/(30•2)=21/60+34/60=(21+34)/60=55/60=(5•11)/(5•12)=11/12 (часть) - резервуара воды откачали оба насоса вместе.
Значит, 1-11/12=12/12-11/12=(12-11)/12=1/12 (часть) - резервуара воды осталось откачать.
Ответ: 1/12 часть.
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







