Упр.2.286 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)
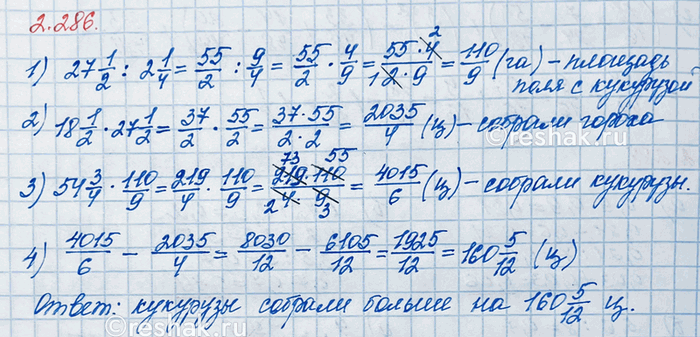
Решение #4 (Учебник 2021)

Решение #5 (Учебник 2021)

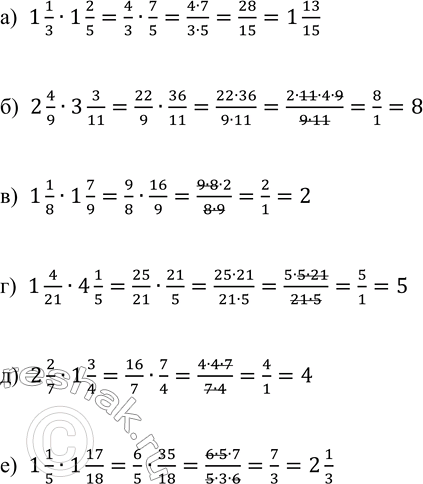
Решение #6 (Учебник 2021)
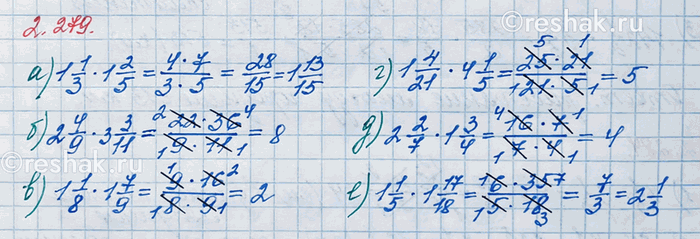
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Урожайность гороха составила 18 1/2 ц с га, а кукурузы — 54 3/4 ц с га. На сколько центнеров больше собрали кукурузы, если площадь поля, засеянного горохом, 27 1/2 га, а площадь поля, засеянного кукурузой, в 2 1/4 раза меньше?
Найдём площадь поля, засеянного кукурузой.
Так как она меньше площади поля с горохом, то найдём её с помощью деления.
27 1/2 :2 1/4=55/2 :9/4=55/2•4/9=(55•4)/(2•9)=(55•2•2)/(2•9)=110/9=12 2/9 (га) – площадь поля, засеянного кукурузой.
Для того, чтобы найти сколько собрали кукурузы, необходимо площадь засеянного ею поля, умножить на урожайность кукурузы.
12 2/9•54 3/4=110/9•219/4=(110•219)/(9•4)=(55•2•3•73)/(3•3•2•2)=4015/6=669 1/6 (ц) – кукурузы собрали.
Для того, чтобы найти сколько собрали гороха, необходимо площадь засеянного им поля, умножить на урожайность гороха.
27 1/2•18 1/2=55/2•37/2=(55•37)/(2•2)=2035/4=508 3/4 (ц) – гороха собрали.
Для того, чтобы определить на сколько центнеров кукурузы собрали больше, чем гороха, необходимо из урожая кукурузы вычесть урожай гороха.
669 1/6-508 3/4=669 (1•2)/(6•2)-508 (3•3)/(4•3)=669 2/12-508 9/12=(668+1+2/12)-508 9/12=(668+12/12+2/12)-508 9/12=(668+(12+2)/12)-508 9/12=(668+14/12)-(508+9/12)=(668-508)+(14/12-9/12)=160+(14-9)/12=160 5/12 (ц).
Ответ: 160 5/12 ц.
Выполните умножение:
а) 1 1/3 · 1 2/5; в) 1 1/8 · 1 7/9; д) 2 2/7 · 1 3/4;
б) 2 4/9 · 3 3/11; г) 1 4/21 · 4 1/5; е) 1 1/5 · 1 17/18.
В примере даны смешанные числа, которые сначала необходимо представить в виде неправильных дробей, для этого нужно знаменатель умножить на целую часть и к полученному результату прибавить числитель, затем, то, что получили, записываем в числитель, знаменатель останется тот же.
Для того, чтобы умножить дробь на дробь, необходимо найти произведение числителей и знаменателей этих дробей. Первое произведение записать числителем, второе – знаменателем.
При умножении необходимо выполнять сокращение, если это возможно, для удобства расчётов. Для этого необходимо одно из чисел числителя и знаменателя разделить на одно и то же число и далее выполнять умножение.
Если при расчётах получается неправильная дробь, необходимо преобразовать её. Для этого нужно числитель разделить на знаменатель, если числитель делится на знаменатель без остатка, то в ответе получаем целое число, если же с остатком, то получим смешанное число, тогда частное пишем в целую часть, остаток – в числитель, знаменатель останется тот же.
а) 1 1/3•1 2/5=4/3•7/5=(4•7)/(3•5)=28/15=1 13/15
б) 2 4/9•3 3/11=22/9•36/11=(22•36)/(9•11)=(2•11•4•9)/(9•11)=8/1=8
в) 1 1/8•1 7/9=9/8•16/9=(9•8•2)/(8•9)=2/1=2
г) 1 4/21•4 1/5=25/21•21/5=(25•21)/(21•5)=(5•5•21)/(21•5)=5/1=5
д) 2 2/7•1 3/4=16/7•7/4=(4•4•7)/(7•4)=4/1=4
е) 1 1/5•1 17/18=6/5•35/18=(6•5•7)/(5•3•6)=7/3=2 1/3
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







