Упр.2.368 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
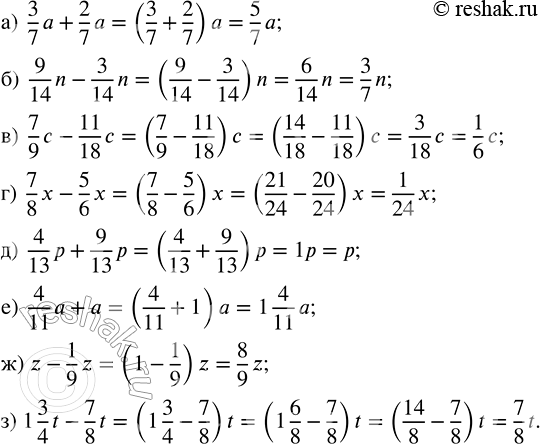
Решение #2 (Учебник 2023)


Решение #3 (Учебник 2023)
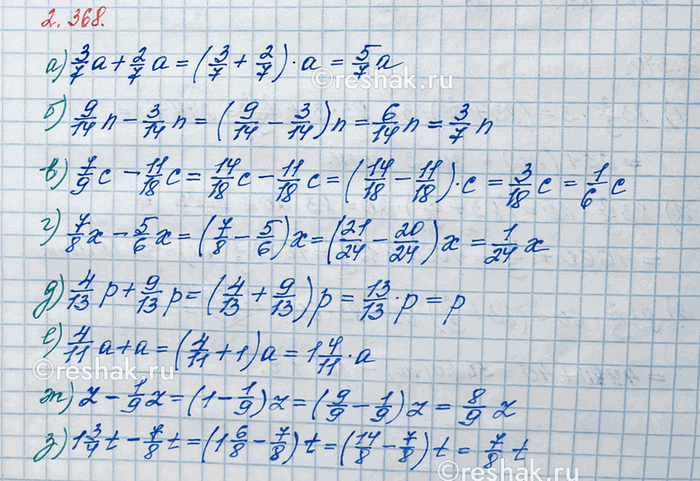
Решение #4 (Учебник 2021)



Решение #5 (Учебник 2021)


Решение #6 (Учебник 2021)
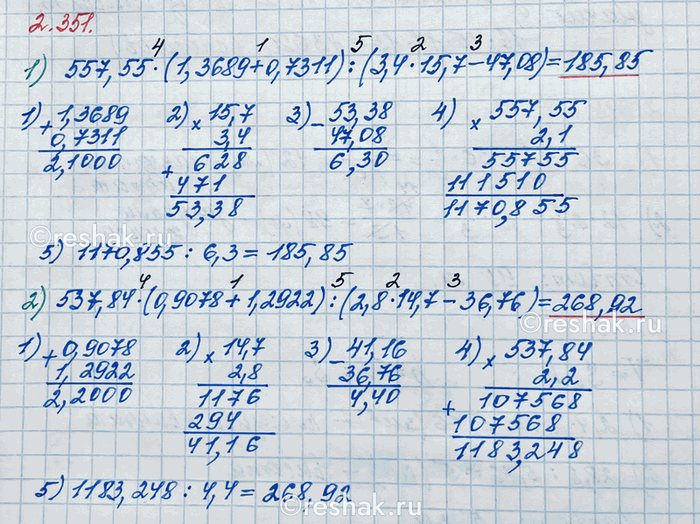
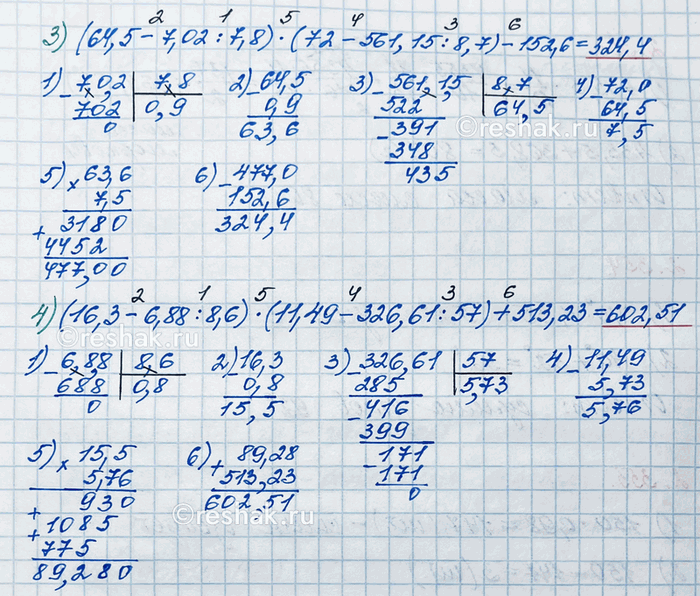
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Упростите выражение:
а) 3/7 a + 2/7 a; в) 7/9 c - 11/18 c; д) 4/13 p + 9/13 p; ж) z - 1/9 z;
б) 9/14 n - 3/14 n; г) 7/8 x - 5/6 x; е) 4/11 a + a; з) 1 3/4 t - 7/8 t.
Используем распределительное свойство умножения относительно сложения и вычитания – выносим общий множитель за скобки.
Если числитель и знаменатель дроби умножить на одно и то же число, то получится дробь, равная исходной.
При сложении (вычитании) дробей с одинаковыми знаменателями, их числители складывают, а знаменатель оставляют тот же.
а) 3/7 a+2/7 a=(3/7+2/7)•a=(3+2)/7 a=5/7 a
б) 9/14 n-3/14 n=(9/14-3/14)•n=(9-3)/14 n=6/14 n=(2•3)/(2•7) n=3/7 n
в) 7/9 c-11/18 c=(7/9-11/18)•c=((7•2)/(9•2)-11/18)c=(14/18-11/18)c=(14-11)/18 c==3/18 c=3/(3•6)c=1/6c
г) 7/8 x-5/6 x=(7/8-5/6)•x=((7•3)/(8•3)-(5•4)/(6•4))x=(21/24-20/24)x=(21-20)/24 x=1/24 x
д) 4/13 p+9/13 p=(4/13+9/13)•p=(4+9)/13 p=13/13 p=1•p=p
е) 4/11 a+a=4/11 a+1•a=(4/11+1)•a=1 4/11 a
ж) z-1/9 z=1•z-1/9 z=(1-1/9)•z=(9/9-1/9)z=(9-1)/9 z=8/9 z
з) 1 3/4 t-7/8 t=(1 3/4-7/8)•t=(1 (3•2)/(4•2)-7/8)t=(1 6/8-7/8)t=((1+6/8)-7/8)t=((8/8+6/8)-7/8)t=((8+6)/8-7/8)t=(14/8-7/8)t=(14-7)/8 t=7/8 t
Вычислите и проверьте вычисления с помощью калькулятора:
1) 557,55 · (1,3689 + 0,7311) : (3,4 · 15,7 - 47,08);
2) 537,84 · (0,9078 + 1,2922) : (2,8 · 14,7 - 36,76);
3) (64,5 - 7,02 : 7,8) · (72 - 561,15 : 8,7) - 152,6;
4) (16,3 - 6,88 : 8,6) · (11,49 - 326,61 : 57) + 513,23.
При выборе порядка выполнения действий опираемся на следующее правило: если в выражении есть скобки, то в первую очередь выполняют действия в скобках, а затем за скобками, причём, как в скобках, так и за скобками, сначала выполняют действия второй ступени (умножение и деление) по порядку слева направо, а потом действия первой ступени (сложение и вычитание), также по порядку слева направо.
При выполнении вычислений опираемся на следующие правила:
- чтобы перемножить две десятичные дроби, необходимо умножить их как натуральные числа, не обращая внимание на запятые; в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
- чтобы разделить десятичную дробь на десятичную, необходимо перенести в делимом и делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе; выполнить деление на натуральное число, а именно, разделить дробь на это число, не обращая внимание на запятую; поставить в частном запятую, когда кончится деление целой части.
1) 557,55•(1,3689+0,7311) :(3,4•15,7-47,08)=557,55•2,1:(3,4•15,7-47,08)=557,55•2,1:(53,38-47,08)=557,55•2,1:6,3=1170,855:6,3=11708,55:63=185,85
2) 537,84•(0,9078+1,2922) :(2,8•14,7-36,76)=537,84•2,2:(2,8•14,7-36,76)=537,84•2,2:(41,16-36,76)=537,84•2,2:4,4=1183,248:4,4=11832,48:44=268,92
3) (64,5-7,02:7,8)•(72-561,15:8,7)-152,6=(64,5-70,2:78)•(72-561,15:8,7)-152,6=(64,5-0,9)•(72-561,15:8,7)-152,6=63,6•(72-561,15:8,7)-152,6=63,6•(72-5611,5:87)-152,6=63,6•(72-64,5)-152,6=63,6•7,5-152,6=477-152,6=324,4
4) (16,3-6,88:8,6)•(11,49-326,61:57)+513,23=(16,3-68,8:86)•(11,49-326,61:57)+513,23=(16,3-0,8)•(11,49-326,61:57)+513,23=15,5•(11,49-326,61:57)+513,23=15,5•(11,49-5,73)+513,23=15,5•5,76+513,23=89,28+513,23=602,51
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







