Упр.2.383 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)
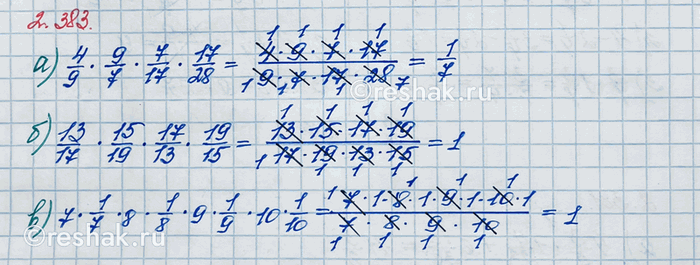
Решение #3 (Учебник 2021)
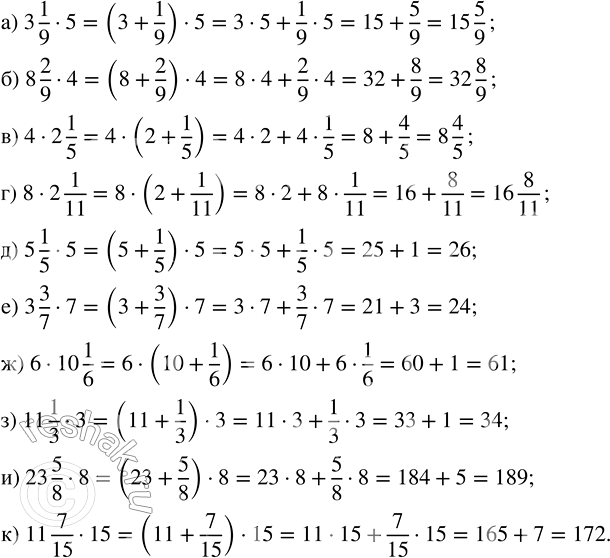
Решение #4 (Учебник 2021)

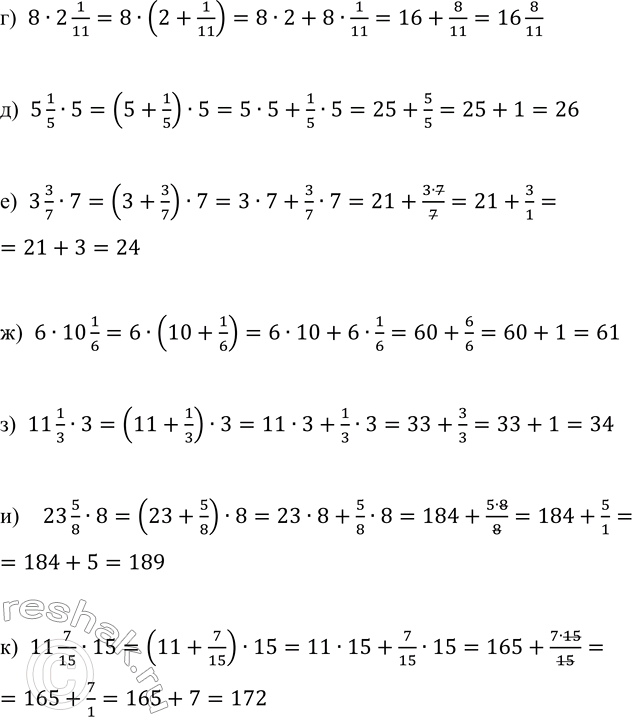
Решение #5 (Учебник 2021)

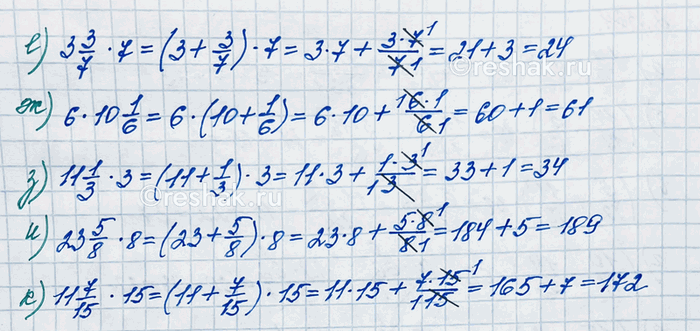
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите произведение:
а) 4/9 · 9/7 · 7/17 · 17/28; б) 13/17 · 15/19 · 17/13 · 19/15;
в) 7 · 1/7 · 8 · 1/8 · 9 · 1/9 · 10 · 1/10.
Найдите произведение:
а) 3 1/9 · 5; в) 4 · 2 1/5; д) 5 1/5 · 5; ж) 6 · 10 1/6; и) 23 5/8 · 8;
б) 8 2/9 · 4; г) 8 · 2 1/11; е) 3 3/7 · 7; з) 11 1/3 · 3; к) 11 7/15 · 15.
Используем распределительное свойство умножения относительно сложения.
Для того, чтобы умножить смешанное число на натуральное число, можно умножить целую часть на натуральное число; умножить дробную часть на это натуральное число; затем сложить полученные результаты.
Для того, чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменений.
Прежде, чем выполнить умножение, выполняем сокращение дробей (если это возможно), то есть делим числитель и знаменатель на одно и то же число (наибольший общий делитель).
Дробь, у которой в знаменателе стоит единица, равна числителю.
а) 3 1/9•5=(3+1/9)•5=3•5+1/9•5=15+5/9=15 5/9
б) 8 2/9•4=(8+2/9)•4=8•4+2/9•4=32+(2•4)/9=32+8/9=32 8/9
в) 4•2 1/5=4•(2+1/5)=4•2+4•1/5=8+4/5=8 4/5
г) 8•2 1/11=8•(2+1/11)=8•2+8•1/11=16+8/11=16 8/11
д) 5 1/5•5=(5+1/5)•5=5•5+1/5•5=25+5/5=25+1=26
е) 3 3/7•7=(3+3/7)•7=3•7+3/7•7=21+(3•7)/7=21+3/1=21+3=24
ж) 6•10 1/6=6•(10+1/6)=6•10+6•1/6=60+6/6=60+1=61
з) 11 1/3•3=(11+1/3)•3=11•3+1/3•3=33+3/3=33+1=34
и) 23 5/8•8=(23+5/8)•8=23•8+5/8•8=184+(5•8)/8=184+5/1==184+5=189
к) 11 7/15•15=(11+7/15)•15=11•15+7/15•15=165+(7•15)/15=165+7/1=165+7=172
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







