Упр.2.388 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)
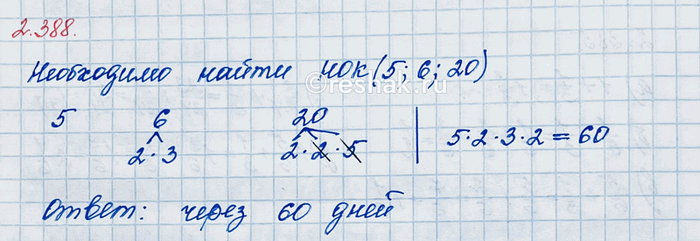
Решение #3 (Учебник 2021)
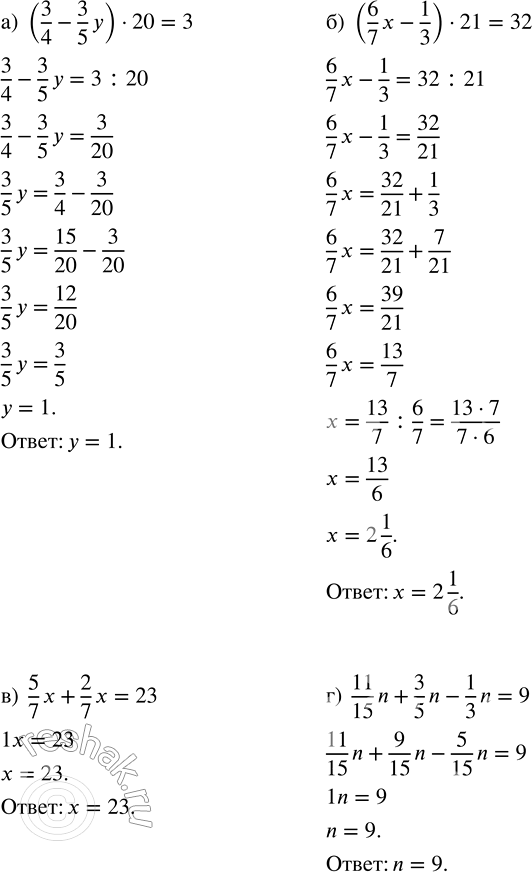
Решение #4 (Учебник 2021)




Решение #5 (Учебник 2021)
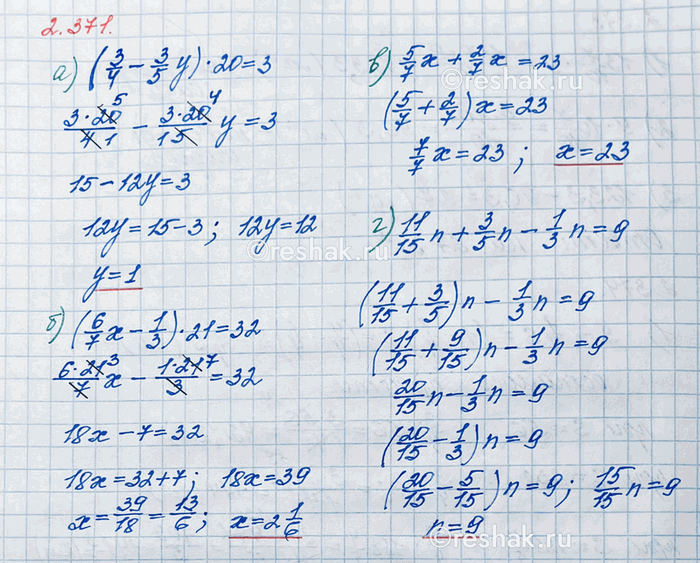
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Корабли возвращаются в порт приписки после каждого рейса. У первого корабля рейс длится 6 дней, у второго — 5 дней, а у третьего — 20 дней. Через сколько дней корабли встретятся в порту, если в первый рейс они вышли одновременно?
Найдите корень уравнения:
а) (3/4 - 3/5 y) · 20 = 3; в) 5/7 x + 2/7 x = 23;
б) (6/7 x - 1/3) · 21 = 32; г) 11/15 n + 3/5 n - 1/3 n = 9.
Уравнение – это равенство, содержащее букву, значение которой необходимо найти.
Корень уравнения – это число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство.
Корень уравнения – это решение уравнения.
Уравнение может иметь один или более корень или не иметь их вообще.
Тогда говорят, что решить уравнение – значит, найти все его корни или показать, что их нет вообще.
Для того, чтобы сложить (вычесть) дроби с разными знаменателями, необходимо привести данные дроби к наименьшему общему знаменателю; затем сложить (вычесть) полученные дроби.
При сложении (вычитании) дробей с одинаковыми знаменателями, их числители складывают, а знаменатель оставляют тот же.
Если числитель и знаменатель дроби умножить на одно и то же число, то получится дробь, равная исходной.
Распределительное свойство умножения - при умножении смешанного числа на натуральное число, можно умножить целую часть на натуральное число; умножить дробную часть на это натуральное число; затем сложить полученные результаты.
а) (3/4-3/5 y)•20=3
Решаем уравнение относительно умножения, то есть неизвестен множитель 3/4-3/5 y.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
3/4-3/5 y=3:20
3/4-3/5 y=3/20
Теперь решаем уравнение относительно вычитания, то есть неизвестно вычитаемое 3/5 y .
Для того, чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность, получим
3/5 y=3/4-3/20
3/5 y=(3•5)/(4•5)-3/20
3/5 y=15/20-3/20
3/5 y=(15-3)/20
3/5 y=12/20
3/5 y=(3•4)/(4•5)
3/5 y=3/5
В полученном уравнении необходимо найти неизвестный множитель y.
y=3/5 :3/5
y=1
б) (6/7 x-1/3)•21=32
Решаем уравнение относительно умножения, то есть неизвестен множитель 6/7 x-1/3 .
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
6/7 x-1/3=32:21
Или, выполнив деление,
6/7 x-1/3=32/21
Решаем полученное уравнение относительно вычитания, то есть неизвестно уменьшаемое 6/7 x .
Для того, чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое, получим
6/7 x=32/21+1/3
6/7 x=32/21+(1•7)/(3•7)
6/7 x=32/21+7/21
6/7 x=(32+7)/21
6/7 x=39/21
В полученном уравнении неизвестен множитель x.
x=39/21 :6/7
x=39/21•7/6
x=(39•7)/(21•6)
x=(3•13•7)/(3•7•2•3)
x=13/6
x=2 1/6
в) 5/7 x+2/7 x=23
(5/7+2/7)•x=23
(5+2)/7 x=23
7/7 x=23
1•x=23
Неизвестен множитель x .
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=23:1
x=23
г) 11/15 n+3/5 n-1/3 n=9
(11/15+3/5-1/3)•n=9
(11/15+(3•3)/(5•3)-(1•5)/(3•5))n=9
(11/15+9/15-5/15)n=9
(11+9-5)/15 n=9
15/15 n=9
1•n=9
Неизвестен множитель n.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
n=9:1
n=9
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







