Упр.2.451 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
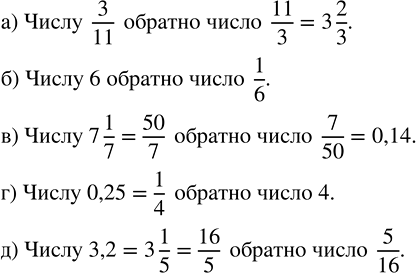
Решение #2 (Учебник 2023)


Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)
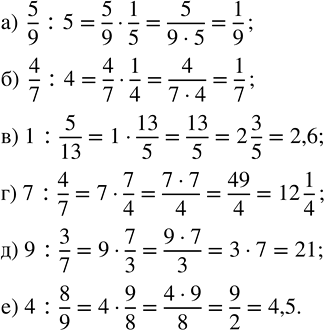
Решение #5 (Учебник 2021)


Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Запишите число, обратное числу:
a) 3/11; б) 6; в) 7 1/7; г) 0,25; д) 3,2.
Два числа, произведение которых равно 1, называются взаимно обратными.
При умножении двух дробей получим единицу, если числитель первой дроби равен знаменателю второй дроби, а знаменатель первой дроби равен числителю второй дроби.
Следовательно, чтобы получить дробь обратную данной, необходимо у данной дроби поменять местами числитель и знаменатель.
а) Дроби 3/11 обратной будет дробь 11/3 которая является неправильной, так как 11>3, значит, её можно преобразовать в смешанное число.
Для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, необходимо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток – как числитель его дробной части.
Тогда, 11/3=3 2/3 , так как 11:3=3 (ост.2).
Следовательно, числу 3/11 обратно число 3 2/3 .
б) 6=6/1 , так как дробь, у которой в знаменателе стоит 1, равна числителю.
Дроби 6/1 обратной будет дробь 1/6 , значит, и числу 6 обратным будет число 1/6 .
в) Для того, чтобы найти число обратное смешанному числу 7 1/7 , его необходимо преобразовать в неправильную дробь.
Для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа, получим
7 1/7=50/7 , так как 7•7+1=49+1=50 .
Дроби 50/7 обратной будет дробь 7/50 , значит, и числу 7 1/7 обратной будет дробь 7/50 .
г) Десятичную дробь всегда можно преобразовать в обыкновенную, у которой в знаменателе стоит единица с нулями (число нулей в знаменателе равно количеству цифр после запятой).
Значит, 0,25=25/100=(25•1)/(25•4)=1/4 , а дроби 1/4 обратной будет дробь 4/1, которая равна 4, так как дробь, у которой в знаменателе стоит 1, равна числителю.
Следовательно, числу 0,25 обратным будет число 4.
д) 3,2=3 2/10=3 (2•1)/(2•5)=3 1/5=16/5 , а дроби 16/5 обратной будет дробь 5/16.
Следовательно, числу 3,2 обратным будет число 5/16 .
Выполните деление:
а) 5/9 : 5; б) 4/7 : 4; в) 1 : 5/13; г) 7 : 4/7; д) 9 : 3/7; е) 4 : 8/9.
При выполнении вычислений опираемся на следующие правила:
- для того, чтобы разделить одну дробь на другую, необходимо делимое умножить на число, обратное делителю, то есть у делителя нужно поменять местами числитель и знаменатель.
- чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменения.
- произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
- при делении дроби на натуральное число, учитываем то, что любое натуральное число можно представить в виде дроби со знаменателем 1, затем пользуемся правилом деления дробей.
При этом, прежде, чем перемножить числа, выполняем сокращение.
Для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, необходимо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток – как числитель его дробной части.
а) 5/9 :5=5/9 :5/1=5/9•1/5=(5•1)/(9•5)=1/9
б) 4/7 :4=4/7 :4/1=4/7•1/4=(4•1)/(7•4)=1/7
в) 1:5/13=1•13/5=13/5=2 3/5=2 (3•2)/(5•2)=2 6/10=2,6
г) 7:4/7=7•7/4=(7•7)/4=49/4=12 1/4
д) 9:3/7=9•7/3=(9•7)/3=(3•3•7)/3=21/1=21
е) 4:8/9=4•9/8=(4•9)/8=(4•9)/(2•4)=9/2=4 1/2=4 (1•5)/(2•5)=4 5/10=4,5
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







