Упр.2.457 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)




Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)

Решение #5 (Учебник 2021)


Решение #6 (Учебник 2021)
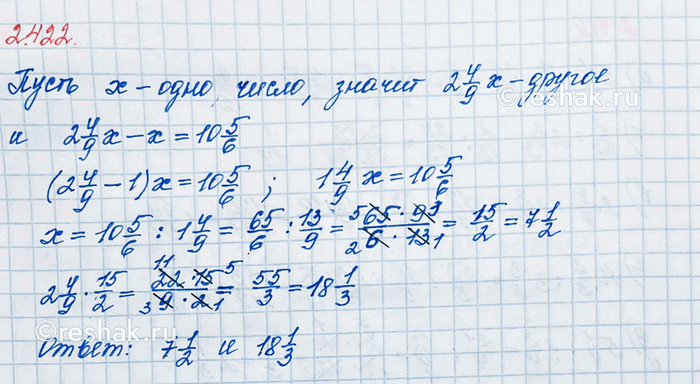
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите корень уравнения:
1) (0,3x + 0,5x) · 4,5 = 10,8; 3) (z - 0,4z) : 0,4 = 1,2;
2) (0,9x - 0,4x) · 7,2 = 10,8; 4) (0,8z + z) : 0,9 = 1,6.
1) (0,3x+0,5x)•4,5=10,8
Сначала решаем уравнение относительно произведения, то есть неизвестен множитель 0,3x+0,5x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
0,3x+0,5x=10,8:4,5
Далее в левой части уравнения используем распределительное свойство умножения относительно сложения, то есть выносим общий множитель x за скобки, а в правой части уравнения переносим запятую у делимого и делителя на один знак вправо, получим (0,3+0,5)x=108:45
Или, выполнив сложение и деление, 0,8x=2,4
В полученном уравнении неизвестен множитель x, значит
x=2,4:0,8
x=24:8
Или, выполнив деление,
x=3
2) (0,9x-0,4x)•7,2=10,8
Сначала решаем уравнение относительно произведения, то есть неизвестен множитель 0,9x-0,4x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
0,9x-0,4x=10,8:7,2
Далее в левой части уравнения используем распределительное свойство умножения относительно вычитания, то есть выносим общий множитель x за скобки, а в правой части уравнения переносим запятую у делимого и делителя на один знак вправо, получим (0,9-0,4)x=108:72
Или, выполнив вычитание и деление,
0,5x=1,5
В полученном уравнении неизвестен множитель x, значит
x=1,5:0,5
x=15:5
Или, выполнив деление,
x=3
3) (z-0,4z) :0,4=1,2
Сначала решаем уравнение относительно деления, то есть неизвестно делимое z-0,4z.
Для того, чтобы найти неизвестное делимое, необходимо частное умножить на делитель, получим
z-0,4z=1,2•0,4
Или, учитывая то, что при умножении единицы на любое число, получим равное ему число, можно записать
1•z-0,4z=1,2•0,4
Далее в левой части уравнения используем распределительное свойство умножения относительно вычитания, то есть выносим общий множитель z за скобки, а в правой части уравнения выполняем умножение, получим
(1-0,4)z=0,48
Или, выполнив вычитание,
0,6z=0,48
В полученном уравнении неизвестен множитель z.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
z=0,48:0,6
z=4,8:6
Или, выполнив деление,
z=0,8
4) (0,8z+z) :0,9=1,6
Сначала решаем уравнение относительно деления, то есть неизвестно делимое 0,8z+z.
Для того, чтобы найти неизвестное делимое, необходимо частное умножить на делитель, получим
0,8z+z=1,6•0,9
Или, учитывая то, что при умножении единицы на любое число, получим равное ему число, можно записать
0,8z+1•z=1,6•0,9
Далее в левой части уравнения используем распределительное свойство умножения относительно сложения, то есть выносим общий множитель z за скобки, а в правой части уравнения выполняем умножение, получим
(0,8+1)z=1,44
Или, выполнив сложение,
1,8z=1,44
В полученном уравнении неизвестен множитель z.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
z=1,44:1,8
z=14,4:18
Или, выполнив деление,
z=0,8
Одно число в 2 4/9 раза больше другого. Найдите эти числа, если их разность равна 10 5/6.
Решим задачу при помощи уравнения.
Пусть x – первое число.
Тогда, второе число 2 4/9 x, так как одно число в 2 4/9 раза больше другого.
При этом разность этих двух чисел равна 10 5/6 .
Следовательно, можем составить следующее уравнение:
2 4/9 x-x=10 5/6
Или, учитывая то, что при умножении единицы на любое число, получим равное ему число,
2 4/9 x-1•x=10 5/6
Далее используем распределительное свойство умножения относительно вычитания, то есть выносим одинаковый множитель x за скобки, получим
(2 4/9-1)x=10 5/6
Или, выполнив вычитание в скобках,
1 4/9 x=10 5/6
Далее решаем уравнение относительно умножения, то есть неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=10 5/6 :1 4/9
Для того, чтобы выполнить деление смешанных чисел, их необходимо перевести в неправильные дроби.
Для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, необходимо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток – как числитель его дробной части, тогда
x=65/6 :13/9
x=65/6•9/13
x=(65•9)/(6•13)
x=(5•13•3•3)/(2•3•13)
x=15/2
x=7 1/2
Для того, чтобы разделить одну обыкновенную дробь на другую, необходимо делимое умножить на число, обратное делителю, то есть у делителя нужно поменять местами числитель и знаменатель.
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
При этом, прежде, чем перемножить числа, выполняем сокращение.
Значит, первое число равно 7 1/2 .
Второе число равно
2 4/9 x=2 4/9•7 1/2=22/9•15/2=(22•15)/(9•2)=(2•11•3•5)/(3•3•2)=55/3=18 1/3
Ответ: 7 1/2; 18 1/3 .
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







