Упр.2.461 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
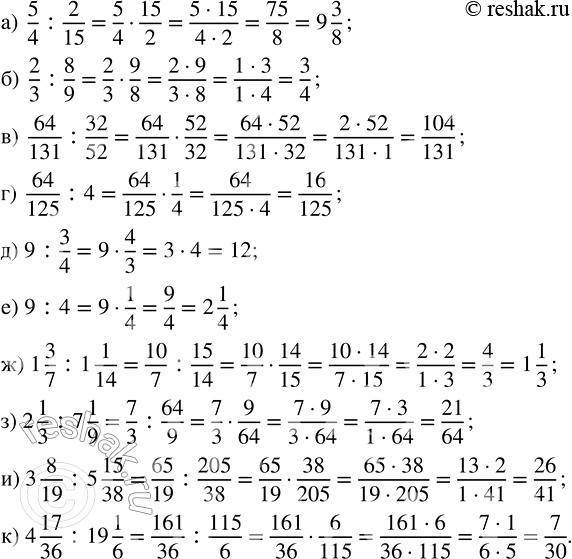
Решение #2 (Учебник 2023)

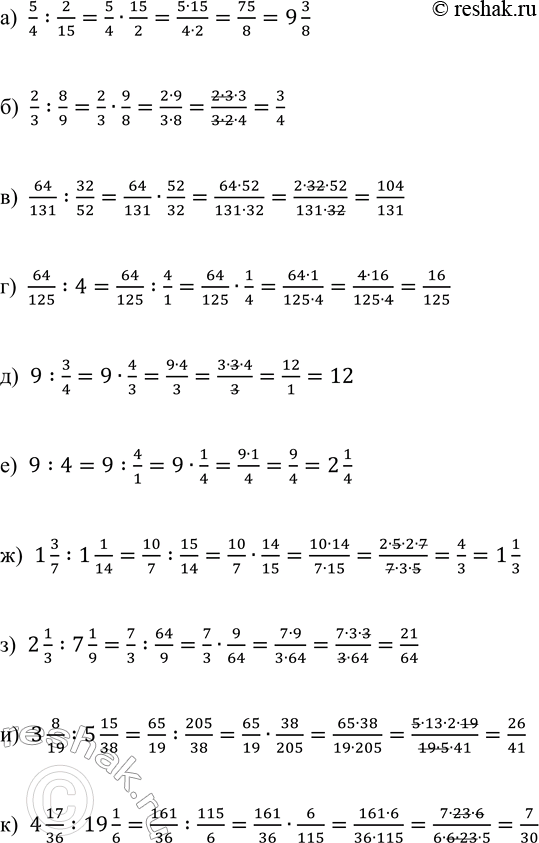
Решение #3 (Учебник 2023)
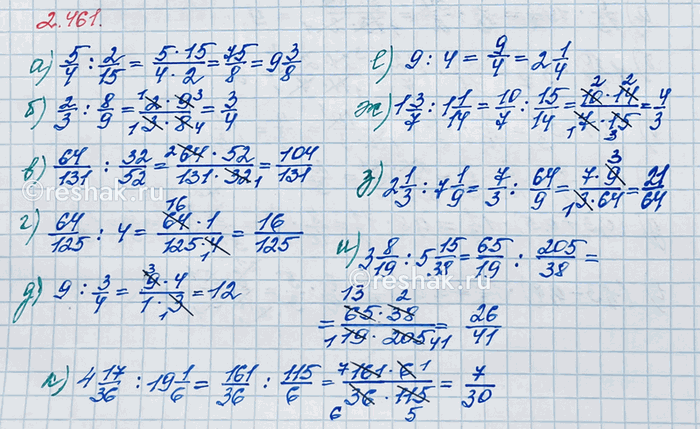
Решение #4 (Учебник 2021)

Решение #5 (Учебник 2021)

Решение #6 (Учебник 2021)
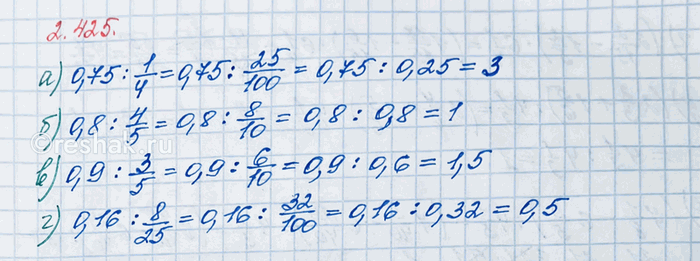
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите частное:
а) 5/4 : 2/15; в) 64/131 : 32/52; д) 9 : 3/4; ж) 1 3/7 : 1 1/14; и) 3 8/19 : 5 15/38;
б) 2/3 : 8/9; г) 64/125 : 4; е) 9 : 4; з) 2 1/3 : 7 1/9; к) 4 17/36 : 19 1/6.
Все вычисления выполняем по следующим правилам:
- для того, чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменения.
- для того, чтобы разделить одну дробь на другую, необходимо делимое умножить на число, обратное делителю, то есть у делителя нужно поменять местами числитель и знаменатель.
- произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
- для того, чтобы выполнить умножение (деление) смешанных чисел, необходимо записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения (деления) дробей.
При этом, прежде, чем перемножить числа, выполняем сокращение.
- для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, необходимо числитель разделить на знаменатель; полученное неполное частное записать, как целую часть смешанного числа, а остаток – как числитель его дробной части.
- для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
а) 5/4 :2/15=5/4•15/2=(5•15)/(4•2)=75/8=9 3/8
б) 2/3 :8/9=2/3•9/8=(2•9)/(3•8)=(2•3•3)/(3•2•4)=3/4
в) 64/131 :32/52=64/131•52/32=(64•52)/(131•32)=(2•32•52)/(131•32)=104/131
г) 64/125 :4=64/125 :4/1=64/125•1/4=(64•1)/(125•4)=(4•16)/(125•4)=16/125
д) 9:3/4=9•4/3=(9•4)/3=(3•3•4)/3=12/1=12
е) 9:4=9:4/1=9•1/4=(9•1)/4=9/4=2 1/4
ж) 1 3/7 :1 1/14=10/7 :15/14=10/7•14/15=(10•14)/(7•15)=(2•5•2•7)/(7•3•5)=4/3=1 1/3
з) 2 1/3 :7 1/9=7/3 :64/9=7/3•9/64=(7•9)/(3•64)=(7•3•3)/(3•64)=21/64
и) 3 8/19 :5 15/38=65/19 :205/38=65/19•38/205=(65•38)/(19•205)=(5•13•2•19)/(19•5•41)=26/41
к) 4 17/36 :19 1/6=161/36 :115/6=161/36•6/115=(161•6)/(36•115)=(7•23•6)/(6•6•23•5)=7/30
Представьте делитель в виде десятичной дроби и найдите частное:
а) 0,75 : 1/4; б) 0,8 : 4/5; в) 0,9 : 3/5; г) 0,16 : 8/25.
Основное свойство обыкновенной дроби – если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится дробь, равная данной.
Для того, чтобы разделить десятичную дробь на десятичную дробь, необходимо перенести в делимом и делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе; выполнить деление на натуральное число.
Для того, чтобы разделить десятичную дробь на натуральное число, необходимо разделить дробь на это число, не обращая внимания на запятую; поставить в частном запятую, когда кончится деление целой части.
Черта в обыкновенной дроби заменяет знак деления, поэтому данное действие всегда можно заменить чертой.
а) 1/4=(1•25)/(4•25)=25/100=0,25
0,75:1/4=0,75:0,25=75:25=3
б) 4/5=(4•2)/(5•2)=8/10=0,8
0,8:4/5=0,8:0,8=8:8=1
в) 3/5=(3•2)/(5•2)=6/10=0,6
0,9:3/5=0,9:0,6=9:6=9/6=(3•3)/(2•3)=1,5
г) 8/25=(8•4)/(25•4)=32/100=0,32
0,16:8/25=0,16:0,32=16:32=16/32=16/(16•2)=1/2=0,5
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







