Упр.2.504 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)

Решение #5 (Учебник 2021)



Решение #6 (Учебник 2021)
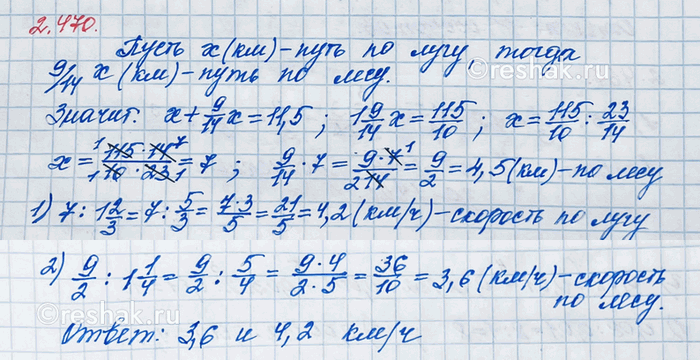
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Элеватор в первый день отгрузил из одной колонны 40 % имеющегося зерна, во второй день — 60 % остатка, а в третий день — 96 т. Сколько зерна было в колонне элеватора?
По условию задачи, в первый день элеватор отгрузил 40% зерна.
Величина, от которой вычисляются проценты составляет 100 своих сотых долей, то есть 100%.
Значит, в колонне осталось 100%-40%=60% зерна.
Также известно, что во второй день отгрузили 60% остатка зерна.
Любое число процентов можно записать в виде десятичной дроби или натурального числа.
Для этого необходимо число, стоящее перед знаком %, разделить на 100.
То есть 60%=60:100=0,60=0,6.
Для того, чтобы найти дробь от числа, необходимо умножить число на эту дробь.
Значит, 0,6 от 60% равно 60•0,6=36,0=36% .
Таким образом, во второй день отгрузили 36% всего зерна.
В первый день отгрузили 40% всего зерна, во второй день – 36% всего зерна, значит, в третий день отгрузили
100%-40%-36%=60%-36%=24% всего зерна.
Известно, что в третий день отгрузили 96 т зерна, что составляет 24% всего зерна.
Для того, чтобы найти число по данному значению его дроби, необходимо это значение разделить на дробь.
24%=24:100=0,24.
Тогда, в колонне элеватора было
96:0,24=9600:24=400 т - зерна.
Ответ: 400 т.
Команда в соревновании по ориентированию на местности прошла маршрут, равный 11,5 км, причём по лугу она шла 1 2/3 ч, а по лесу — 1 1/4 ч. Путь по лесу составлял 9/14 пути по лугу. Найдите скорости передвижения команды по лесу и по лугу.
Решаем задачу при помощи уравнения.
Пусть по лугу команда шла x км.
Тогда, 9/14 x км команда шла по лесу, так как путь по лесу составлял 9/14 пути по лугу, а, чтобы найти дробь от числа, необходимо число умножить на эту дробь.
При этом весь маршрут команды составил 11,5 км.
Следовательно, можно составить следующее уравнение
x+9/14 x=11,5
Или, учитывая то, что при умножении единицы на любое число, получим равное ему число, можно записать,
1•x+9/14 x=11,5
Далее используем распределительное свойство умножения относительно сложения, то есть выносим общий множитель x за скобки, получим,
(1+9/14)x=11,5
Или, выполнив сложение в скобках,
1 9/14 x=11,5
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=11,5:1 9/14
В полученном уравнении десятичную дробь представим как смешанное число 11 5/10=11 (5•1)/(5•2)=11 1/2 , а затем преобразуем оба смешанных числа в неправильные дроби.
Для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа, получим
11 1/2=23/2 , так как 11•2+1=22+1=23 .
1 9/14=23/14 , так как 1•14+9=14+9=23 .
Для того, чтобы разделить две обыкновенные дроби, необходимо делимое умножить на число, обратное делителю, то есть у делителя поменять местами числитель и знаменатель, получим
x=23/2•14/23
Произведением двух дробей является число, числитель которого равен произведению числителей, а знаменатель - произведению знаменателей, тогда
x=(23•14)/(2•23)
Или, выполнив сокращение,
x=(2•7)/2
x=7/1
Дробь, у которой в знаменателе стоит единица, равна числителю.
Значит, x=7.
Следовательно, по лугу команда прошла 7 км.
Весь маршрут команды составил 11,5 км, 7 км из которого путь по лугу.
Значит, путь по лесу составил
11,5-7=4,5 км.
Для того, чтобы найти скорость движения, необходимо пройденный путь разделить на время в пути.
За 1 2/3 часа по лугу команда прошла 7 км, значит, скорость движения команды по лугу равна
7:1 2/3=7:5/3=7•3/5=(7•3)/5=21/5=4 1/5=4 (1•2)/(5•2)=4 2/10=4,2 км/ч.
За 1 1/4 часа по лесу команда прошла 4,5 км, значит, скорость движения команды по лесу равна
4,5:1 1/4=4,5:1 (1•25)/(4•25)=4,5:1 25/100=4,5:1,25=450:125=3,6 км/ч.
Ответ: 4,2 км/ч – скорость по лугу; 3,6 км/ч – скорость по лесу.
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







