Упр.2.62 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
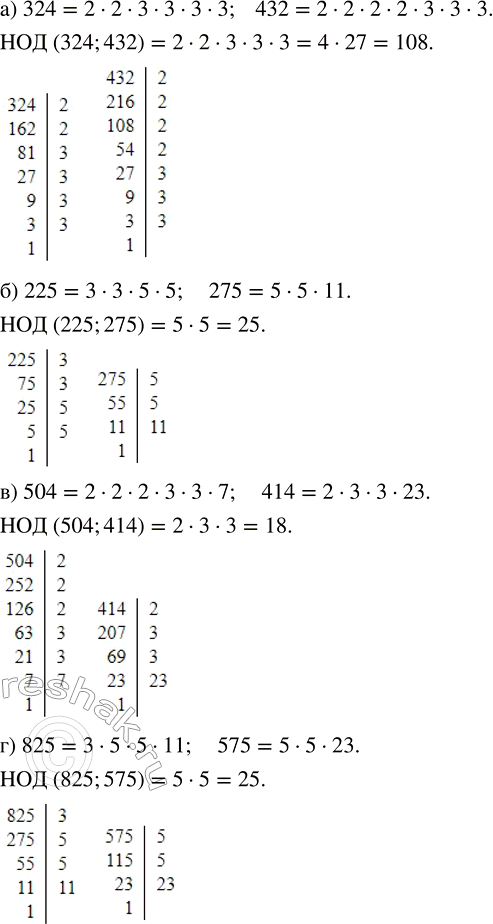
Решение #2 (Учебник 2023)


Решение #3 (Учебник 2021)

Решение #4 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите наибольший общий делитель чисел:
а) 324 и 432; б) 225 и 275; в) 504 и 414; г) 825 и 575.
а) Разложим числа 324 и 432 на простые множители и подчеркнём общие множители чисел.
324=2•2•3•3•3•3
432=2•2•2•2•3•3•3
Общие множители чисел: 2; 2; 3; 3; 3.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (324;432)=2•2•3•3•3=4•27=108
б) Разложим числа 225 и 275 на простые множители и подчеркнём общие множители чисел.
225=3•3•5•5
275=5•5•11
Общие множители чисел: 5; 5.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (225;275)=5•5=25
в) Разложим числа 504 и 414 на простые множители и подчеркнём общие множители чисел.
504=2•2•2•3•3•7
414=2•3•3•23
Общие множители чисел: 2; 3; 3.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (504;414)=2•3•3=6•3=18
г) Разложим числа 825 и 575 на простые множители и подчеркнём общие множители чисел.
825=3•5•5•11
575=5•5•23
Общие множители чисел: 5; 5.
Для того чтобы найти НОД чисел, необходимо перемножить их общие множители.
НОД (825;575)=5•5=25
Разложите каждое число на простые множители, зачеркните общие множители и запишите наибольшее число, на которое делятся числа каждой пары:
а) 36 и 48; б) 84 и 96; в) 45 и 60; г) 72 и 90.
Наибольшим общим делителем (НОД) нескольких чисел называют наибольшее натуральное число, на которое делятся эти числа без остатка.
Для того, чтобы найти наибольший общий делитель нескольких натуральных чисел, необходимо:
- разложить их на простые множители;
- из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
- найти произведение оставшихся множителей.
а) 36 и 48
36=2•2•3•3
48=2•2•2•2•3
НОД (36,48)=2•2•3=12
б) 84 и 96
84=2•2•3•7
96=2•2•2•2•2•3
НОД (84,96)=2•2•3=12
в) 45 и 60
45=3•3•5
60=2•2•3•5
НОД (45,60)=3•5=15
г) 72 и 90
72=2•2•2•3•3
90=2•3•3•5
НОД (72,90)=2•3•3=18
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







