Упр.7.21 ГДЗ Погорелов 7-9 класс (Геометрия)
Решение #1
Рассмотрим вариант решения задания из учебника Погорелов 8 класс, Просвещение:
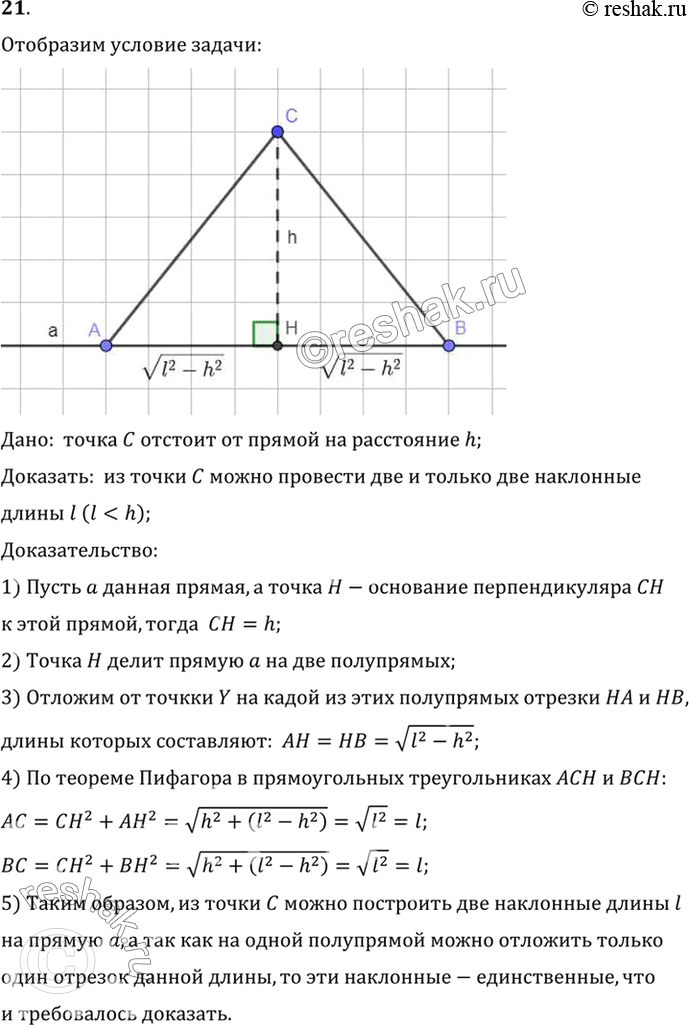
21. Даны прямая и точка С на расстоянии h от этой прямой. Докажите, что из точки С можно провести две и только две наклонные длины l, если l > h (рис. 165).
Дано: точка C отстоит от прямой на расстояние h;
Доказать: из точки C можно провести две и только две наклонные
длины l (l < h);
Доказательство:
1) Пусть a данная прямая, а точка H-основание перпендикуляра CH
к этой прямой, тогда CH=h;
2) Точка H делит прямую a на две полупрямых;
3) Отложим от точкки Y на кадой из этих полупрямых отрезки HA и HB,
длины которых составляют: AH=HB=v(l^2-h^2);
4) По теореме Пифагора в прямоугольных треугольниках ACH и BCH:
AC=CH^2+AH^2=v(h^2+(l^2-h^2))=v(l^2)=l;
BC=CH^2+BH^2=v(h^2+(l^2-h^2))=v(l^2)=l;
5) Таким образом, из точки C можно построить две наклонные длины l
на прямую a, а так как на одной полупрямой можно отложить только
один отрезок данной длины, то эти наклонные-единственные, что
и требовалось доказать.
Популярные решебники 8 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением





