Упр.2.172 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
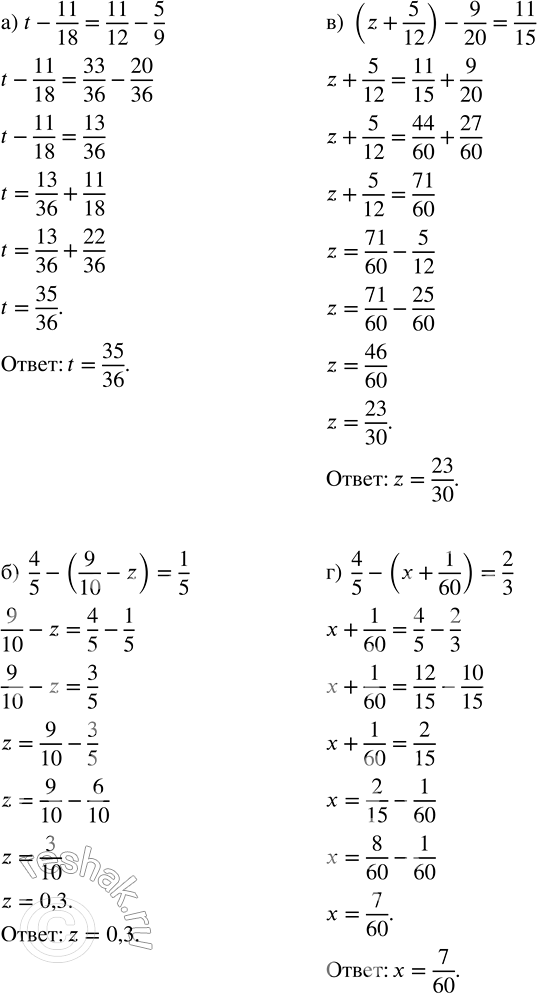
Решение #2 (Учебник 2023)



Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)
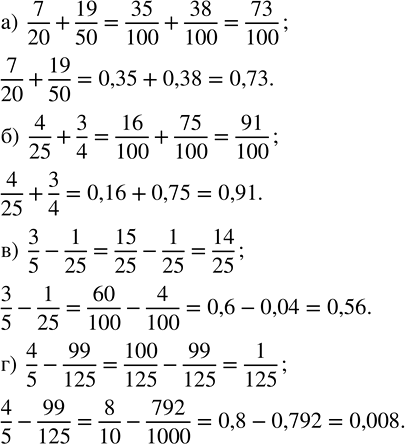
Решение #5 (Учебник 2021)




Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Решите уравнение:
а) t - 11/18 = 11/12 - 5/9; в) (z + 5/12) - 9/20 = 11/15;
б) 4/5 - (9/10 - z) = 1/5; г) 4/5 - (x + 1/60) = 2/3.
Для того, чтобы сложить (вычесть) дроби с одинаковыми знаменателями, необходимо сложить (вычесть) их числители, а знаменатель оставить прежним.
Если числитель и знаменатель дроби умножить на одно и то же число, то получится дробь, равная исходной.
а) t-11/18=11/12-5/9
Выполним вычитание в правой части выражения.
t-11/18=(11•3)/(12•3)-(5•4)/(9•4)
t-11/18=33/36-20/36
t-11/18=(33-20)/36
t-11/18=13/36
В уравнении неизвестно уменьшаемое t.
Для того, чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое, получим
t=13/36+11/18
t=13/36+(11•2)/(18•2)
t=13/36+22/36
t=(13+22)/36
t=35/36
б) 4/5-(9/10-z)=1/5
В уравнении неизвестно вычитаемое 9/10-z.
Для того, чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность, получим
9/10-z=4/5-1/5
9/10-z=(4-1)/5
9/10-z=3/5
В уравнении вновь неизвестно вычитаемое z, получим
z=9/10-3/5
z=9/10-(3•2)/(5•2)
z=9/10-6/10
z=(9-6)/10
z=3/10=0,3
в) (z+5/12)-9/20=11/15
В уравнении неизвестно уменьшаемое z+5/12.
Для того, чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое, получим
z+5/12=11/15+9/20
z+5/12=(11•4)/(15•4)+(9•3)/(20•3)
z+5/12=44/60+27/60
z+5/12=(44+27)/60
z+5/12=71/60
В уравнении неизвестно слагаемое z.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим
z=71/60-5/12
z=71/60-(5•5)/(12•5)
z=71/60-25/60
z=(71-25)/60
z=46/60=(2•23)/(2•30)=23/30
г) 4/5-(x+1/60)=2/3
В уравнении неизвестно вычитаемое x+1/60.
Для того, чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность, получим
x+1/60=4/5-2/3
x+1/60=(4•3)/(5•3)-(2•5)/(3•5)
x+1/60=12/15-10/15
x+1/60=(12-10)/15
x+1/60=2/15
В уравнении неизвестно слагаемое x.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим
x=2/15-1/60
x=(2•4)/(15•4)-1/60
x=8/60-1/60
x=(8-1)/60
x=7/60
Вычислите сначала в обыкновенных дробях, а потом в десятичных:
а) 7/20 + 19/50; б) 4/25 + 3/4; в) 3/5 - 1/25; г) 4/5 - 99/125.
Для того, чтобы сложить (вычесть) дроби с одинаковыми знаменателями, необходимо сложить (вычесть) их числители, а знаменатель оставить прежним.
Если числитель и знаменатель дроби умножить на одно и то же число, то получится дробь, равная исходной.
а) 7/20+19/50=(7•5)/(20•5)+(19•2)/(50•2)=35/100+38/100=(35+38)/100=73/100
В записи десятичными дробями.
Для того, чтобы дробь 7/20 представить в виде десятичной дроби, сначала расширяем эту дробь на число 5 (дополнительный множитель), чтобы в знаменателе получилась разрядная единица 100.
7/20=(7•5)/(20•5)=35/100
Для того, чтобы получившуюся дробь записать в виде десятичной дроби, сначала пишем целую часть, а потом числитель дробной части (0,35).
Для того, чтобы дробь 19/50 представить в виде десятичной дроби, сначала расширяем эту дробь на число 2 (дополнительный множитель), чтобы в знаменателе получилась разрядная единица 100.
19/50=(19•2)/(50•2)=38/100
Для того, чтобы получившуюся дробь записать в виде десятичной дроби, сначала пишем целую часть, а потом числитель дробной части (0,38).
Теперь выполняем сложение.
0,35+0,38=0,73
б) 4/25+3/4=(4•4)/(25•4)+(3•25)/(4•25)=16/100+75/100=(16+75)/100=91/100
В записи десятичными дробями.
Для того, чтобы дробь 4/25 представить в виде десятичной дроби, сначала расширяем эту дробь на число 4 (дополнительный множитель), чтобы в знаменателе получилась разрядная единица 100.
4/25=(4•4)/(25•4)=16/100
Для того, чтобы получившуюся дробь записать в виде десятичной дроби, сначала пишем целую часть, а потом числитель дробной части (0,16).
Для того, чтобы дробь 3/4 представить в виде десятичной дроби, сначала расширяем эту дробь на число 25 (дополнительный множитель), чтобы в знаменателе получилась разрядная единица 100.
3/4=(3•25)/(4•25)=75/100
Для того, чтобы получившуюся дробь записать в виде десятичной дроби, сначала пишем целую часть, а потом числитель дробной части (0,75).
Теперь выполняем сложение.
0,16+0,75=0,91
в) 3/5-1/25=(3•5)/(5•5)-1/25=15/25-1/25=(15-1)/25=14/25
В записи десятичными дробями.
Для того, чтобы дробь 3/5 представить в виде десятичной дроби, сначала расширяем эту дробь на число 2 (дополнительный множитель), чтобы в знаменателе получилась разрядная единица 10.
3/5=(3•2)/(5•2)=6/10
Для того, чтобы получившуюся дробь записать в виде десятичной дроби, сначала пишем целую часть, а потом числитель дробной части (0,6).
Для того, чтобы дробь 1/25 представить в виде десятичной дроби, сначала расширяем эту дробь на число 4 (дополнительный множитель), чтобы в знаменателе получилась разрядная единица 100.
1/25=(1•4)/(25•4)=4/100
Для того, чтобы получившуюся дробь записать в виде десятичной дроби, сначала пишем целую часть, а потом числитель дробной части (0,04).
После запятой должно стоять столько знаков, сколько нулей было в знаменателе обыкновенной дроби (100 – два нуля).
Так как в числителе однозначное число 4, а должно быть два знака после запятой, то вместо недостающего знака ставим число 0.
Теперь выполняем вычитание.
0,6-0,04=0,60-0,04=0,56
г) 4/5-99/125=(4•25)/(5•25)-99/125=100/125-99/125=(100-99)/125=1/125
В записи десятичными дробями.
Для того, чтобы дробь 4/5 представить в виде десятичной дроби, сначала расширяем эту дробь на число 2 (дополнительный множитель), чтобы в знаменателе получилась разрядная единица 10.
4/5=(4•2)/(5•2)=8/10
Для того, чтобы получившуюся дробь записать в виде десятичной дроби, сначала пишем целую часть, а потом числитель дробной части (0,8).
Для того, чтобы дробь 99/125 представить в виде десятичной дроби, сначала расширяем эту дробь на число 8 (дополнительный множитель), чтобы в знаменателе получилась разрядная единица 1000.
99/125=(99•8)/(125•8)=792/1000
Для того, чтобы получившуюся дробь записать в виде десятичной дроби, сначала пишем целую часть, а потом числитель дробной части (0,792).
Теперь выполняем вычитание.
0,8-0,792=0,800-0,792=0,008
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







