Упр.2.174 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
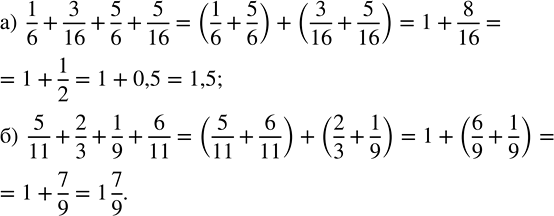
Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)
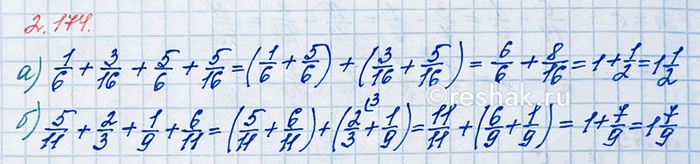
Решение #4 (Учебник 2021)
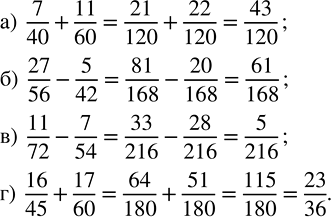
Решение #5 (Учебник 2021)

Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите сумму:
а) 1/6 + 3/16 + 5/6 + 5/16; б) 5/11 + 2/3 + 1/9 + 6/11.
При сложении дробей с одинаковыми знаменателями, числители складывают, а знаменатель оставляют тот же.
а) Для выражения 1/6+3/16+5/6+5/16 применяем сочетательный и переместительный законы сложения (при сложении нескольких чисел законы сложения позволяют переставлять слагаемые и расставлять скобки так, как нам удобно для вычислений).
Сгруппируем слагаемые отдельно со знаменателем 6, и отдельно со знаменателем 16.
1/6+3/16+5/6+5/16=(1/6+5/6)+(3/16+5/16)
(1/6+5/6)+(3/16+5/16)=(1+5)/6+(3+5)/16=6/6+8/16=1+8/16
Сократим дробь на 8.
1+8/16=1+(8•1)/(8•2)=1+1/2=1 1/2
б) Для выражения 5/11+2/3+1/9+6/11 применяем сочетательный и переместительный законы сложения (при сложении нескольких чисел законы сложения позволяют переставлять слагаемые и расставлять скобки так, как нам удобно для вычислений).
Сгруппируем слагаемые отдельно со знаменателем 11, и отдельно со знаменателями 3 и 9.
5/11+2/3+1/9+6/11=(5/11+6/11)+(2/3+1/9)
(5/11+6/11)+(2/3+1/9)=(5+6)/11+(2/3+1/9)=11/11+(2/3+1/9)=1+(2/3+1/9)
В скобках приведём дроби к общему знаменателю 9.
1+(2/3+1/9)=1+((2•3)/(3•3)+1/9)=1+(6/9+1/9)=1+(6+1)/9=1+7/9=1 7/9
Найдите значение выражения:
а) 7/40 + 11/60; б) 27/56 - 5/42; в) 11/72 - 7/54; г) 16/45 + 17/60.
Для того, чтобы сложить (вычесть) дроби с одинаковыми знаменателями, необходимо сложить (вычесть) их числители, а знаменатель оставить прежним.
Если числитель и знаменатель дроби умножить на одно и то же число, то получится дробь, равная исходной.
а) 7/40+11/60=(7•3)/(40•3)+(11•2)/(60•2)=21/120+22/120=(21+22)/120=43/120
б) 27/56-5/42=(27•3)/(56•3)-(5•4)/(42•4)=81/168-20/168=(81-20)/168=61/168
в) 11/72-7/54=(11•3)/(72•3)-(7•4)/(54•4)=33/216-28/216=(33-28)/216=5/216
г) 16/45+17/60=(16•4)/(45•4)+(17•3)/(60•3)=64/180+51/180=(64+51)/180=115/180=(5•23)/(5•36)=23/36
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







