Упр.2.436 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
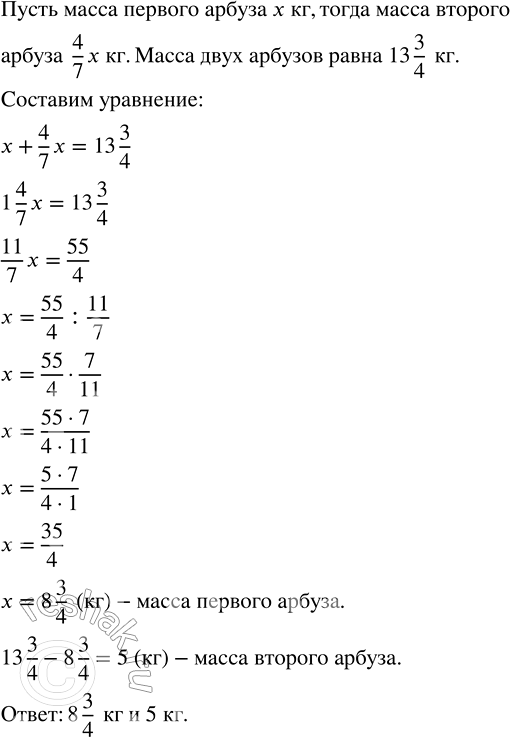
Решение #2 (Учебник 2023)


Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)

Решение #5 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Масса двух арбузов равна 13 3/4 кг. При этом масса одного арбуза составляет 4/7 массы другого арбуза. Чему равна масса каждого арбуза?
Решаем задачу при помощи уравнения.
Пусть x кг масса первого арбуза.
Тогда, масса второго арбуза 4/7 x кг, так как масса второго арбуза составляет 4/7 массы первого арбуза.
При этом масса двух арбузов равна 13 3/4 кг.
Следовательно, можно составить следующее уравнение
4/7 x+x=13 3/4 , или, учитывая то, что при умножении единицы на любое число, получим равное ему число, можно записать
4/7 x+1•x=13 3/4
Далее преобразуем полученное уравнение, используя распределительное свойство умножения относительно сложения, то есть выносим одинаковый множитель x за скобки, получим
(4/7+1)x=13 3/4
Для того, чтобы найти сумму двух смешанных чисел, необходимо отдельно сложить их целые и дробные части.
Тогда, выполнив сложение в скобках, получим
1 4/7 x=13 3/4
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=13 3/4 :1 4/7
Для того, чтобы выполнить деление, сначала представим смешанные числа в виде неправильных дробей.
Для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части, эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа, получим
13 3/4=55/4 , так как 13•4+3=52+3=55
1 4/7=11/7 , так как 1•7+4=7+4=11 .
Тогда, x=55/4 :11/7 .
Для того, чтобы разделить две обыкновенные дроби, необходимо делимое умножить на число, обратное делителю, то есть у делителя поменять местами числитель и знаменатель, получим
x=55/4•7/11
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей, тогда
x=(55•7)/(4•11)
x=(5•11•7)/(4•11)
Или, выполнив сокращение, x=(5•7)/4
Или, выполнив умножение в числителе, x=35/4
Значит, x=8 3/4.
Следовательно, масса первого арбуза, 8 3/4 кг.
Масса двух арбузов 13 3/4 кг, масса первого арбуза 8 3/4 кг.
Значит, масса второго арбуза равна
13 3/4-8 3/4=(13-8)+(3/4-3/4)=5+0=5 кг.
Ответ: 5 кг и 8 3/4 кг.
Запишите в виде неправильной дроби числа 2 1/3, 1 9/11, 3 1/8, 9 1/13, 5.
Для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
2 1/3=7/3 , так как 2•3+1=6+1=7
1 9/11=20/11 , так как 1•11+9=11+9=20
3 1/8=25/8 , так как 3•8+1=24+1=25
9 1/13=118/13 , так как 9•13+1=117+1=118
При этом частное двух натуральных чисел равно дроби, числитель которой – делимое, а знаменатель – делитель.
Значит, всякое натуральное число может быть записано в виде дроби, причём натуральное число можно представить в виде дроби с каким угодно знаменателем.
Тогда, учитывая то, что 20:4=5, получим 5=20/4 .
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







