Упр.2.440 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)


Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)
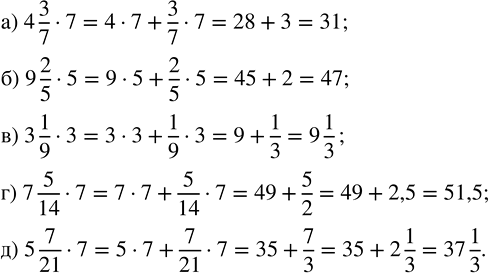
Решение #5 (Учебник 2021)


Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Пёс Барбос с хозяином ехали на автобусе 3 ч со скоростью 76 км/ч, затем 12 ч — ехали на поезде и 2 ч шли пешком со скоростью, в 19 раз меньшей скорости автобуса. Найдите их среднюю скорость передвижения, если скорость автобуса составляет 1 1/3 скорости поезда.
Для того, чтобы найти пройденный путь, необходимо скорость движения умножить на время в пути.
Пёс Барбос с хозяином ехали на автобусе 3 часа со скоростью 76 км/ч, значит, на автобусе они проехали 76•3=228 км.
Далее они 12 часов ехали на поезде.
Скорость автобуса составляет 1 1/3 скорости поезда, то есть скорость поезда равна
76:1 1/3=76:4/3=76•3/4=(76•3)/4=(4•19•3)/4=57/1=57 км/ч.
Для того, чтобы разделить натуральное число на обыкновенную дробь, необходимо делимое умножить на число, обратное делителю, то есть у делителя поменять местами числитель и знаменатель.
Для того, чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменений.
Дробь, у которой в знаменателе стоит единица, равна числителю.
Значит, двигаясь на поезде со скоростью 57 км/ч, за 12 часов пёс с хозяином проехали 57•12=684 км.
Затем они 2 часа шли пешком со скоростью в 19 раз меньшей скорости автобуса.
Значит, их скорость пешком составила 76:19=4 км/ч.
Следовательно, пешком они прошли 4•2=8 км.
Для того, чтобы найти среднюю скорость движения, необходимо весь пройденный путь разделить на всё время движения.
Пёс Барбос с хозяином на автобусе проехали 228 км, на поезде - 684 км и прошли пешком 8 км.
Значит, весь путь, проделанный ими, равен
228+684+8=912+8=920 км.
Пёс Барбос с хозяином ехали на автобусе 3 часа, 12 часов ехали на поезде и 2 часа шли пешком.
Значит, их общее время в пути равно
3+12+2=15+2=17 часов.
Следовательно, средняя скорость передвижения пса с хозяином равна 920:17=920/17=54 2/17 км/ч.
Ответ: 54 2/17 км/ч.
Найдите произведение:
а) 4 3/7 · 7; б) 9 2/5 · 5; в) 3 1/9 · 3; г) 7 5/14 · 7; д) 5 7/21 · 7.
Для того, чтобы умножить смешанное число на натуральное, можно умножить целую часть на натуральное число, умножить дробную часть на натуральное число, сложить полученные результаты.
Для того, чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменения
Также учитываем то, что дробь, у которой в знаменателе стоит единица, равна числителю и, прежде чем перемножать числа, выполняем сокращение.
а) 4 3/7•7=(4+3/7)•7=4•7+3/7•7=28+(3•7)/7=28+3/1=28+3=31
б) 9 2/5•5=(9+2/5)•5=9•5+2/5•5=45+(2•5)/5=45+2/1=45+2=47
в) 3 1/9•3=(3+1/9)•3=3•3+1/9•3=9+3/9=9+(3•1)/(3•3)=9+1/3=9 1/3
г) 7 5/14•7=(7+5/14)•7=7•7+5/14•7=49+(5•7)/14=49+(5•7)/(7•2)=49+5/2=49+2,5=51,5
д) 5 7/21•7=(5+7/21)•7=5•7+7/21•7=35+(7•7)/21=35+(7•7)/(3•7)=35+7/3=35+2 1/3=37 1/3
Для того, чтобы неправильную дробь (7/3), числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, необходимо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток – как числитель его дробной части.
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







