Упр.2.438 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
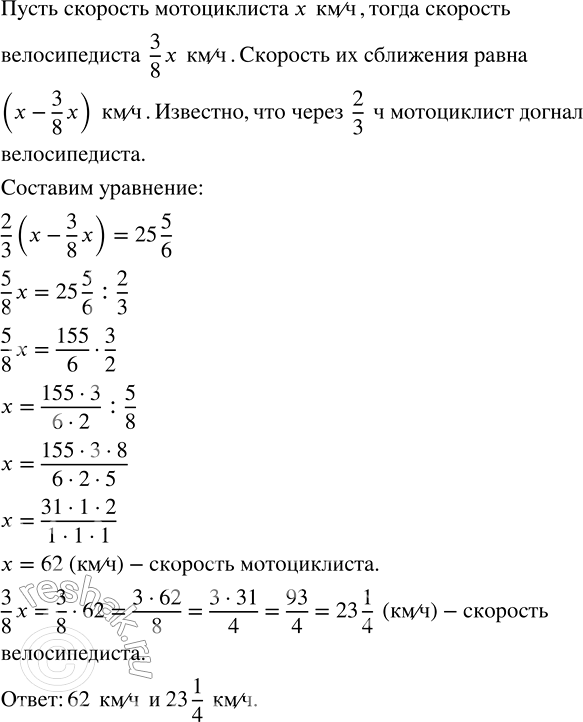
Решение #2 (Учебник 2023)



Решение #3 (Учебник 2023)
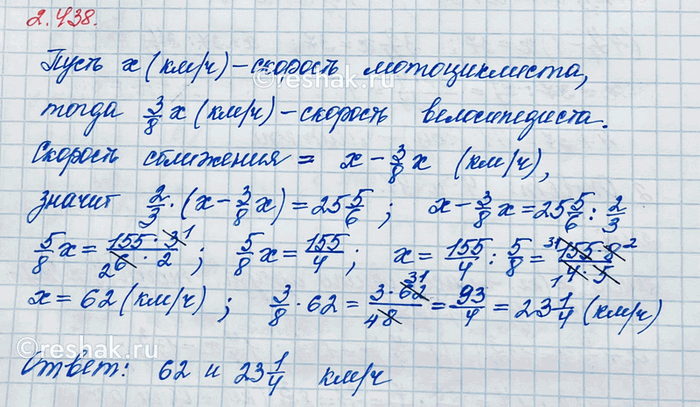
Решение #4 (Учебник 2021)

Решение #5 (Учебник 2021)


Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Когда велосипедист отъехал от лагеря на 25 5/6 км, из лагеря выехал мотоциклист и догнал его через 2/3 ч. Скорость велосипедиста составляла 3/8 скорости мотоциклиста. Найдите скорости мотоциклиста и велосипедиста.
Решаем задачу при помощи уравнения.
Пусть x км/ч – скорость мотоциклиста.
Тогда, 3/8 x км/ч – скорость велосипедиста, так как скорость велосипедиста составляла 3/8 скорости мотоциклиста, а, чтобы найти дробь от числа, необходимо умножить число на эту дробь.
Мотоциклист догонял велосипедиста, то есть они двигались в одном направлении и сближались.
Тогда, скорость сближения мотоциклиста с велосипедистом составляет x-3/8 x км/ч, или, учитывая то, что при умножении единицы на любое число, получим равное ему число, можно записать 1•x-3/8 x км/ч.
Далее используем распределительное свойство умножения относительно вычитания, то есть выносим общий множитель x за скобки, получим, что скорость сближения мотоциклиста с велосипедистом равна (1-3/8)x.
Для того, чтобы выполнить вычитание в скобках, используем то, что единицу можно представить в виде дроби, у которой в числителе и знаменателе стоят одинаковые числа, тогда скорость сближения будет равна (8/8-3/8)x км/ч, или (8-3)/8 x км/ч,
или 5/8 x км/ч, так как чтобы найти разность двух дробей с одинаковыми знаменателями, необходимо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.
Для того, чтобы найти расстояние, необходимо скорость умножить на время.
Между мотоциклистом и велосипедистом было 25 5/6км, сближаясь со скоростью 5/8 x км/ч, мотоциклист догнал велосипедиста через 2/3 часа.
Следовательно, можно составить следующее уравнение
5/8 x•2/3=25 5/6
В левой части полученного уравнения используем сочетательное свойство умножения, тогда получим
5/8•2/3 x=25 5/6
Смешанное число 25 5/6 преобразуем в неправильную дробь.
Для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа, получим
25 5/6=155/6 , так как 25•6+5=150+5=155 .
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей, получим
(5•2)/(8•3) x=155/6
Или, выполнив сокращение,
(5•2)/(2•4•3) x=155/6
5/12 x=155/6
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=155/6 :5/12
Для того, чтобы выполнить деление обыкновенных дробей, необходимо делимое умножить на число, обратное делителю, то есть у делителя поменять местами числитель и знаменатель, получим
x=155/6•12/5
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей, тогда
x=(155•12)/(6•5)
Или, выполнив сокращение,
x=(5•31•6•2)/(6•5)
x=62/1
Дробь, у которой в знаменателе стоит единица, равна числителю.
Значит, x=62.
Следовательно, скорость мотоциклиста 62 км/ч.
Скорость велосипедиста составляла 3/8 скорости мотоциклиста, а, чтобы найти дробь от числа, необходимо умножить число на эту дробь.
Значит, скорость велосипедиста равна
62•3/8=(62•3)/8=(2•31•3)/(2•4)=93/4=23 1/4 км/ч.
Ответ: 23 1/4 км/ч и 62 км/ч.
Проверьте вычисления:
а) 15 · 2 1/5 = 15 · 2 + 15 : 5 = 30 + 3 = 33;
б) 24 · 4 1/4 = 24 · 4 + 24 : 4 = 96 + 6 = 102;
в) 36 · 2/3 = 36 + 36 : 3 = 36 + 12 = 48;
г) 98 · 6/7 = 98 - 98 : 7 = 98 - 14 = 84.
Ответ обьясните.
В пунктах а) и б) для проверки используем следующее правило:
- для того, чтобы умножить смешанное число на натуральное, можно умножить целую часть на натуральное число, умножить дробную часть на натуральное число (чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменения), сложить полученные результаты.
Тогда,
а) 15•2 1/5=15•(2+1/5)=15•2+15•1/5=30+15/5=30+(5•3)/5=30+3/1=30+3=33 – верно.
б) 24•4 1/4=24•(4+1/4)=24•4+24•1/4=96+24/4=96+(4•6)/4=96+6/1=96+6=102 - верно.
В пунктах в) и г) для проверки используем то, что единицу можно представить в виде неправильной дроби, у которой числитель и знаменатель одинаковые.
в) 1-1/3=3/3-1/3=(3-1)/3=2/3
Тогда, 36•2/3=36•(1-1/3)=36•1-36•1/3=36-36/3=
=36-36:3=36-12=24
Используем распределительное свойство умножения относительно вычитания, то есть умножаем число, стоящее перед скобками, на каждый компонент стоящий в скобках и вычитаем результаты умножения.
Также при вычислениях учитываем то, что частное двух натуральных чисел равно дроби, числитель которой – делимое, а знаменатель – делитель, поэтому 36/3=36:3.
Значит, 36•2/3=48 – неверно.
г) 1-1/7=7/7-1/7=(7-1)/7=6/7
Тогда, 98•6/7=98•(1-1/7)=98•1-98•1/7=98-98/7=
=98-98:7=98-14=84
Используем распределительное свойство умножения относительно вычитания, то есть умножаем число, стоящее перед скобками, на каждый компонент стоящий в скобках и вычитаем результаты умножения.
Также при вычислениях учитываем то, что частное двух натуральных чисел равно дроби, числитель которой – делимое, а знаменатель – делитель, поэтому 98/7=98:7.
Значит, 98•6/7=84 – верно.
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







