Упр.4.287 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)


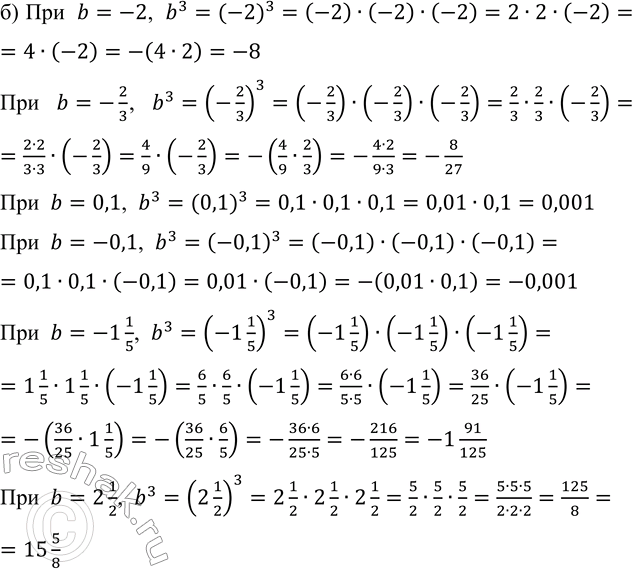
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Вычислите значение:
а) p^2 при p = -4; p = -1/9; p = 0,6; p = -0,8; p = -2 1/3; p = 3 1/5;
б) b^3 при b = -2; b = -2/3; b = 0,1; b = -0,1; b = -1 1/5; b = 2 1/2.
Для того, чтобы найти значение буквенного выражения при заданном числовом значении буквы, необходимо в это выражение вместо буквы подставить соответствующее этой букве числовое значение и выполнить вычисления.
Для того, чтобы число возвести в степень, необходимо умножить это число само на себя столько раз, какова его степень.
При выполнении вычислений опираемся на следующие правила:
- для того, чтобы перемножить два числа с разными знаками, необходимо умножить их модули и перед полученным произведением поставить знак «-».
- для того, чтобы перемножить два отрицательных числа, необходимо перемножить их модули.
- произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
- для того, чтобы выполнить умножение смешанных чисел, необходимо записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
- для того, чтобы перемножить две десятичные дроби, необходимо умножить их как натуральные числа, не обращая внимание на запятые; в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
Для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
Если при выполнении вычислений получаем неправильную дробь, то преобразуем эту дробь в смешанное число.
Для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, необходимо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток – как числитель его дробной части.
а) При p=-4, p^2=(-4)^2=(-4)•(-4)=4•4=16
При p=-1/9, p^2=(-1/9)^2=(-1/9)•(-1/9)=1/9•1/9=(1•1)/(9•9)=1/81
При p=0,6, p^2=(0,6)^2=0,6•0,6=0,36
При p=-0,8, p^2=(-0,8)^2=(-0,8)•(-0,8)=0,8•0,8=0,64
При p=-2 1/3, p^2=(-2 1/3)^2=(-2 1/3)•(-2 1/3)=2 1/3•2 1/3=7/3•7/3=(7•7)/(3•3)=49/9=5 4/9
При p=3 1/5, p^2=(3 1/5)^2=(3 1/5)•(3 1/5)=3 1/5•3 1/5=16/5•16/5=(16•16)/(5•5)=256/25=10 6/25=10 (6•4)/(25•4)=10 24/100=10,24
б) При b=-2, b^3=(-2)^3=(-2)•(-2)•(-2)=2•2•(-2)==4•(-2)=-(4•2)=-8
При b=-2/3, b^3=(-2/3)^3=(-2/3)•(-2/3)•(-2/3)=2/3•2/3•(-2/3)==(2•2)/(3•3)•(-2/3)=4/9•(-2/3)=-(4/9•2/3)=-(4•2)/(9•3)=-8/27
При b=0,1, b^3=(0,1)^3=0,1•0,1•0,1=0,01•0,1=0,001
При b=-0,1, b^3=(-0,1)^3=(-0,1)•(-0,1)•(-0,1)=0,1•0,1•(-0,1)=0,01•(-0,1)=-(0,01•0,1)=-0,001
При b=-1 1/5, b^3=(-1 1/5)^3=(-1 1/5)•(-1 1/5)•(-1 1/5)=
=1 1/5•1 1/5•(-1 1/5)=6/5•6/5•(-1 1/5)=(6•6)/(5•5)•(-1 1/5)=36/25•(-1 1/5)=-(36/25•1 1/5)=-(36/25•6/5)=-(36•6)/(25•5)=-216/125=-1 91/125
При b=2 1/2, b^3=(2 1/2)^3=2 1/2•2 1/2•2 1/2=5/2•5/2•5/2=(5•5•5)/(2•2•2)=125/8=15 5/8
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







