Упр.5.51 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)

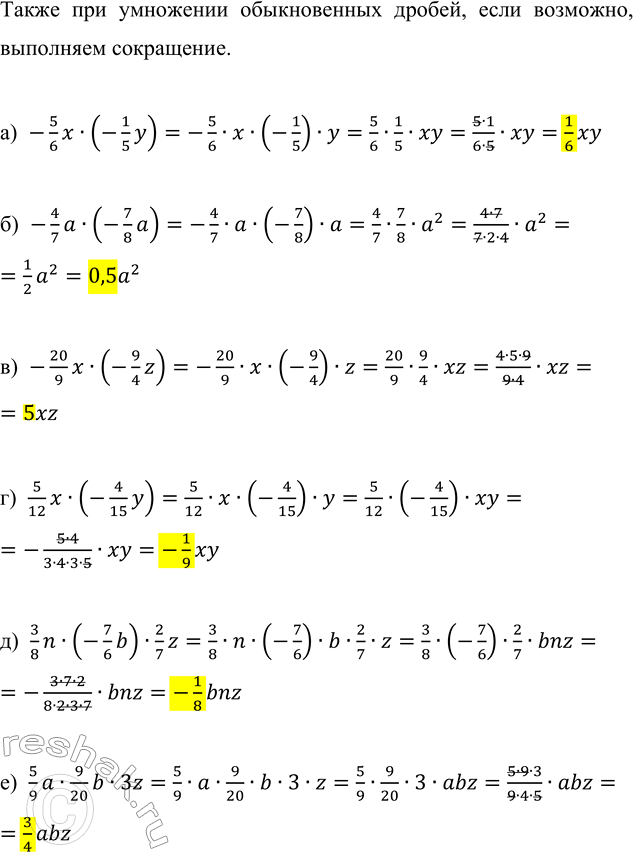
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите произведение и подчеркните коэффициент:
а) -5/6 x · (-1/5 y); в) -20/9 x · (-9/4 z); д) 3/8 n · (-7/6 b) · 2/7 z;
б) -4/7 a · (-7/8 a); г) 5/12 x · (-4/15 y); е) 5/9 a · 9/20 b · 3z.
При упрощении выражений используем переместительное и сочетательное свойства умножения рациональных чисел, то есть множители в произведениях меняем местами и расставляем скобки так, чтобы можно было выполнить умножение чисел, имеющихся в произведениях.
Число, которое получится после умножения всех чисел в произведении, является коэффициентом (его выделяем).
При выполнении умножения опираемся на следующие правила:
- для того, чтобы перемножить два числа с разными знаками, необходимо умножить их модули и перед полученным произведением поставить знак «-».
- для того, чтобы перемножить два отрицательных числа, необходимо перемножить их модули.
- для того, чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменения.
- произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
Также при умножении обыкновенных дробей, если возможно, выполняем сокращение.
а) -5/6 x•(-1/5 y)=-5/6•x•(-1/5)•y=5/6•1/5•xy=(5•1)/(6•5)•xy=1/6 xy
б) -4/7 a•(-7/8 a)=-4/7•a•(-7/8)•a=4/7•7/8•a^2=(4•7)/(7•2•4)•a^2=1/(2) a^2=0,5a^2
в) -20/9 x•(-9/4 z)=-20/9•x•(-9/4)•z=20/9•9/4•xz=(4•5•9)/(9•4)•xz=5xz
г) 5/12 x•(-4/15 y)=5/12•x•(-4/15)•y=5/12•(-4/15)•xy=-(5•4)/(3•4•3•5)•xy=-1/9 xy
д) 3/8 n•(-7/6 b)•2/7 z=3/8•n•(-7/6)•b•2/7•z=3/8•(-7/6)•2/7•bnz=-(3•7•2)/(8•2•3•7)•bnz=-1/8 bnz
е) 5/9 a•9/20 b•3z=5/9•a•9/20•b•3•z=5/9•9/20•3•abz=(5•9•3)/(9•4•5)•abz=3/4 abz
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







