Упр.5.418 ГДЗ Виленкин Жохов 5 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)
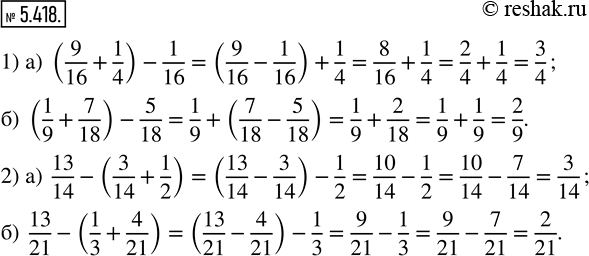
Решение #2 (Учебник 2023)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Александрова 5 класс, Просвещение:
1) Вычислите, используя свойство вычитания числа из суммы:
а) (9/16 + 1/4) - 1/16; б) (1/9 + 7/18) - 5/18.
2) Вычислите, используя свойство вычитания суммы из числа:
а) 13/14 - (3/14 + 1/2); б) 13/21 - (1/3 + 4/21).
1) Для того, чтобы из суммы вычесть число, можно вычесть его из одного слагаемого, а к полученной разности прибавить другое слагаемое.
а) (9/16+1/4)-1/16=(9/16-1/16)+1/4=(9-1)/16+1/4=8/16+1/4=(2•4)/(4•4)+1/4=2/4+1/4=(2+1)/4=3/4
Сократим дробь 8/16 , разделив числитель и знаменатель на их общий делитель, отличный от единицы (4).
б) (1/9+7/18)-5/18=(7/18-5/18)+1/9=(7-5)/18+1/9=2/18+1/9=(2•1)/(2•9)+1/9=1/9+1/9=(1+1)/9=2/9
Сократим дробь 2/18 , разделив числитель и знаменатель на их общий делитель, отличный от единицы (2).
2) Для того, чтобы вычесть сумму из числа, можно сначала вычесть из этого числа первое слагаемое, а потом из полученной разности вычесть второе слагаемое.
а) 13/14-(3/14+1/2)=(13/14-3/14)-1/2=(13-3)/14-1/2=10/14-1/2=10/14-(1•7)/(2•7)=10/14-7/14=(10-7)/14=3/14
Приведём дроби к общему знаменателю (14), использовав основное свойство дроби - если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится равная ей дробь.
б) 13/21-(1/3+4/21)=(13/21-4/21)-1/3=(13-4)/21-1/3=9/21-1/3=9/21-(1•7)/(3•7)=9/21-7/21=(9-7)/21=2/21
Приведём дроби к общему знаменателю (21), использовав основное свойство дроби.
Популярные решебники 5 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







