Упр.4.215 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)
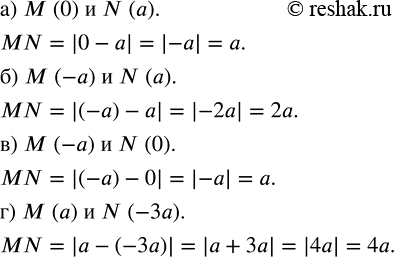
Решение #2 (Учебник 2023)


Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите расстояние между точками М и N координатной прямой:
а) М (0) и N (a); б) М (-а) и N (a); в) M (-а) и N (0); г) М (а) и N (-3a).
Для того, чтобы найти расстояние от 0 до какого-то числа на координатной прямой (отрицательного или положительного), необходимо найти модуль этого числа, так как модулем числа a называют расстояние (в единичных отрезках) от начала координат до точки A(a).
Тогда, расстояние между отрицательным и положительным числами на координатной прямой будет равно сумме модулей этих чисел, так как отрицательные числа находятся слева от нуля, а положительные – справа.
а) M(0) и N(a)
|a|=a
Значит, расстояние между точками M и N, то есть между 0 и a, равно a единичных отрезков.
б) M(-a) и N(a)
|-a|=a, |a|=a
a+a=2a
Значит, расстояние между точками M и N, то есть между -a и a, равно 2a единичных отрезков.
в) M(-a) и N(0)
|-a|=a
Значит, расстояние между точками M и N, то есть между -a и 0, равно a единичных отрезков.
г) M(a) и N(-3a)
|a|=a, |-3a|=3a
a+3a=4a
Значит, расстояние между точками M и N, то есть между a и -3a, равно 4a единичных отрезков.
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







