Упр.4.217 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)


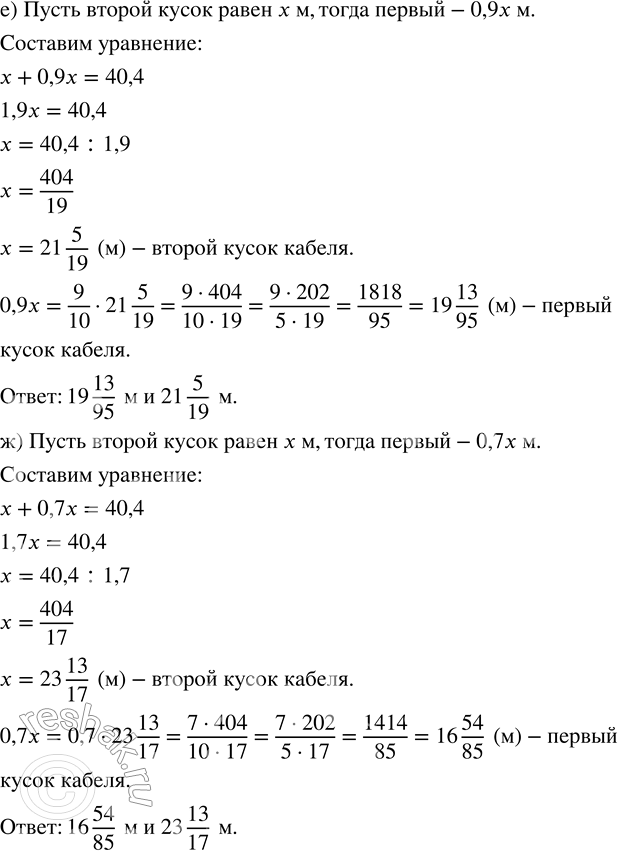

Решение #2 (Учебник 2023)






Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Составьте уравнение для решения задачи: «Кабель длиной 40,4 м разделили на два куска. Найдите длину каждого куска, если известно, что один из кусков:
а) на 0,9 м длиннее другого;
Пусть длина первого куска кабеля равна x м, тогда длина второго куска кабеля равна x+0,9 м, так как по условию один из кусков кабеля на 0,9 м длиннее другого.
При этом первоначально кабель был длиной 40,4 м.
Следовательно, можно составить следующее уравнение
x+x+0,9=40,4
Или, учитывая то, что при умножении единицы на любое число, получим равное ему число, можно записать
1•x+1•x+0,9=40,4
Далее используем распределительное свойство умножения относительно сложения, то есть выносим одинаковый множитель x за скобки, получим (1+1)x+0,9=40,4
Или, выполнив сложение в скобках 2x+0,9=40,4
Теперь полученное уравнение решаем относительно сложения, то есть неизвестно слагаемое 2x.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим 2x=40,4-0,9 .
Или, выполнив вычитание, 2x=39,5 .
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=39,5:2
Или, выполнив деление, x=19,75 .
Значит, длина первого куска кабеля равна 19,75 м.
Длина второго куска кабеля на 0,9 м больше длины первого куска, значит, длина второго куска кабеля равна
19,75+0,9=20,65 (м).
Ответ: 19,75 м и 20,65 м.
б) на 0,3 м короче другого;
Пусть длина первого куска кабеля равна x м, тогда длина второго куска кабеля равна x+0,3 м, так как по условию один из кусков кабеля на 0,3 м короче другого, то есть второй кусок кабеля на 0,3 м больше, чем первый.
При этом первоначально кабель был длиной 40,4 м.
Следовательно, можно составить следующее уравнение
x+x+0,3=40,4
Или, учитывая то, что при умножении единицы на любое число, получим равное ему число, можно записать
1•x+1•x+0,3=40,4
Далее используем распределительное свойство умножения относительно сложения, то есть выносим одинаковый множитель x за скобки, получим (1+1)x+0,3=40,4
Или, выполнив сложение в скобках 2x+0,3=40,4
Теперь полученное уравнение решаем относительно сложения, то есть неизвестно слагаемое 2x.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим 2x=40,4-0,3 .
Или, выполнив вычитание, 2x=40,1 .
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=40,1:2
Или, выполнив деление, x=20,05 .
Значит, длина первого куска кабеля равна 20,05 м.
Длина второго куска кабеля на 0,3 м больше длины первого куска, значит, длина второго куска кабеля равна
20,05+0,3=20,35 (м).
Ответ: 20,05 м и 20,35 м.
в) в 4 раза длиннее другого;
Пусть длина первого куска кабеля равна x м, тогда длина второго куска кабеля равна 4x м, так как по условию один из кусков кабеля в 4 раза длиннее другого.
При этом первоначально кабель был длиной 40,4 м.
Следовательно, можно составить следующее уравнение
x+4x=40,4
Или, учитывая то, что при умножении единицы на любое число, получим равное ему число, можно записать 1•x+4x=40,4
Далее используем распределительное свойство умножения относительно сложения, то есть выносим одинаковый множитель x за скобки, получим (1+4)x=40,4
Или, выполнив сложение в скобках 5x=40,4
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=40,4:5
Или, выполнив деление, x=8,08 .
Значит, длина первого куска кабеля равна 8,08 м.
Длина второго куска кабеля в 4 раза длиннее первого куска, значит, длина второго куска кабеля равна 4•8,08=32,32 (м).
Ответ: 8,08 м и 32,32 м.
г) в 2,5 раза короче другого;
Пусть длина первого куска кабеля равна x м, тогда длина второго куска кабеля равна 2,5x м, так как по условию один из кусков кабеля в 2,5 раза короче другого, то есть второй кусок в 2,5 раза больше первого куска кабеля.
При этом первоначально кабель был длиной 40,4 м.
Следовательно, можно составить следующее уравнение
x+2,5x=40,4
Или, учитывая то, что при умножении единицы на любое число, получим равное ему число, можно записать 1•x+2,5x=40,4
Далее используем распределительное свойство умножения относительно сложения, то есть выносим одинаковый множитель x за скобки, получим (1+2,5)x=40,4
Или, выполнив сложение в скобках 3,5x=40,4
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=40,4:3,5 или x=404:35
Или, выполнив сокращение, x=404/35
x=11 19/35 .
Значит, длина первого куска кабеля равна 11 19/35 м.
Длина второго куска кабеля в 2,5 раза длиннее первого куска, значит, длина второго куска кабеля равна
2,5•11 19/35=2 5/10•404/35=2 (5•1)/(2•5)•404/35=5/2•404/35=(5•2•202)/(2•5•7)=28 6/7 (м).
Ответ: 11 19/35 м и 28 6/7 м.
д) составляет 3/4 другого;
Пусть длина первого куска кабеля равна x м, тогда длина второго куска кабеля равна 3/4 x м, так как по условию один из кусков кабеля составляет 3/4 длины другого, а чтобы найти дробь от числа, необходимо число умножить на эту дробь.
При этом первоначально кабель был длиной 40,4 м.
Следовательно, можно составить следующее уравнение
x+3/4 x=40,4
Или, учитывая то, что при умножении единицы на любое число, получим равное ему число, можно записать 1•x+3/4 x=40,4
Далее используем распределительное свойство умножения относительно сложения, то есть выносим одинаковый множитель x за скобки, получим (1+3/4)x=40,4
Или, выполнив сложение в скобках 1 3/4 x=40,4
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=40,4:1 3/4
Для того, чтобы выполнить деление, смешанное число 1 3/4 представим в виде неправильной дроби.
Для этого необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа, получим 1 3/4=7/4 , тогда x=40,4:7/4
Для того, чтобы разделить число на обыкновенную дробь, необходимо делимое умножить на число, обратное делителю, то есть у делителя поменять местами числа, стоящие в числителе и знаменателе дроби, получим x=40,4•4/7=(404•4)/70
Или, выполнив сокращение, x=1616/70=(2•808)/(2•35)
x=23 3/35 .
Значит, длина первого куска кабеля равна 23 3/35 м.
Тогда, длина второго куска кабеля равна
3/4•23 3/35=3/4•808/35=(3•808)/(4•35)=(3•4•202)/(4•35)=606/35=17 11/35 (м).
Ответ: 23 3/35 м и 17 11/35 м.
е) составляет 0,9 другого;
Пусть длина первого куска кабеля равна x м, тогда длина второго куска кабеля равна 0,9x м, так как по условию один из кусков кабеля составляет 0,9 длины другого, а чтобы найти дробь от числа, необходимо число умножить на эту дробь.
При этом первоначально кабель был длиной 40,4 м.
Следовательно, можно составить следующее уравнение
x+0,9x=40,4
Или, учитывая то, что при умножении единицы на любое число, получим равное ему число, можно записать 1•x+0,9x=40,4
Далее используем распределительное свойство умножения относительно сложения, то есть выносим одинаковый множитель x за скобки, получим (1+0,9)x=40,4
Или, выполнив сложение в скобках 1,9x=40,4
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=40,4:1,9 или x=404:19
Или, x=404/19
x=21 5/19 .
Значит, длина первого куска кабеля равна 21 5/19 м.
Тогда, длина второго куска кабеля равна
0,9•21 5/19=9/10•404/19=(9•2•202)/(2•5•19)=1818/95=19 13/95 (м).
Ответ: 21 5/19 м и 19 13/95 м.
ж) составляет 70 % другого;
Любое число процентов можно записать в виде десятичной дроби или натурального числа.
Для этого необходимо число, стоящее перед знаком %, разделить на 100.
Тогда, 70%=70:100=0,70=0,7.
При выполнении деления учитываем то, что любое натуральное число можно представить в виде десятичной дроби с каким угодно количеством нулей после запятой, то есть у натурального числа запятую подразумеваем, но не пишем, на конце справа.
Для того, чтобы разделить десятичную дробь на 100, необходимо в этой дроби перенести запятую влево на 2 цифры.
Также учитываем то, что если в десятичной дроби последние цифры – нули, то, отбросив их, получим дробь, равную данной.
Значит, длина второго куска кабеля составляет 0,7 первого куска.
Пусть длина первого куска кабеля равна x м, тогда длина второго куска кабеля равна 0,7x м, так как по условию один из кусков кабеля составляет 0,7 длины другого, а чтобы найти дробь от числа, необходимо число умножить на эту дробь.
При этом первоначально кабель был длиной 40,4 м.
Следовательно, можно составить следующее уравнение
x+0,7x=40,4
Или, учитывая то, что при умножении единицы на любое число, получим равное ему число, можно записать 1•x+0,7x=40,4
Далее используем распределительное свойство умножения относительно сложения, то есть выносим одинаковый множитель x за скобки, получим (1+0,7)x=40,4
Или, выполнив сложение в скобках 1,7x=40,4
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=40,4:1,7 или x=404:17
Или, x=404/17
x=23 13/17 .
Значит, длина первого куска кабеля равна 23 13/17 м.
Тогда, длина второго куска кабеля равна
0,7•23 13/17=7/10•404/17=(7•2•202)/(2•5•17)=1414/85=16 54/85 (м).
Ответ: 23 13/17 м и 16 54/85 м.
з) составляет 230 % другого».
Любое число процентов можно записать в виде десятичной дроби или натурального числа.
Для этого необходимо число, стоящее перед знаком %, разделить на 100.
Тогда, 230%=230:100=2,30=2,3.
При выполнении деления учитываем то, что любое натуральное число можно представить в виде десятичной дроби с каким угодно количеством нулей после запятой, то есть у натурального числа запятую подразумеваем, но не пишем, на конце справа.
Для того, чтобы разделить десятичную дробь на 100, необходимо в этой дроби перенести запятую влево на 2 цифры.
Также учитываем то, что если в десятичной дроби последние цифры – нули, то, отбросив их, получим дробь, равную данной.
Значит, длина второго куска кабеля составляет 2,3 первого куска.
Пусть длина первого куска кабеля равна x м, тогда длина второго куска кабеля равна 2,3x м, так как по условию один из кусков кабеля составляет 2,3 длины другого, а чтобы найти дробь от числа, необходимо число умножить на эту дробь.
При этом первоначально кабель был длиной 40,4 м.
Следовательно, можно составить следующее уравнение
x+2,3x=40,4
Или, учитывая то, что при умножении единицы на любое число, получим равное ему число, можно записать 1•x+2,3x=40,4
Далее используем распределительное свойство умножения относительно сложения, то есть выносим одинаковый множитель x за скобки, получим (1+2,3)x=40,4
Или, выполнив сложение в скобках 3,3x=40,4
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=40,4:3,3 или x=404:33
Или, x=404/33
x=12 8/33 .
Значит, длина первого куска кабеля равна 12 8/33 м.
Тогда, длина второго куска кабеля равна
2,3•12 8/33=2 3/10•12 8/33=23/10•404/33=(23•2•202)/(2•5•33)=4646/165=28 26/165 (м).
Ответ: 12 8/33 м и 28 26/165 м.
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







