Упр.4.226 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)
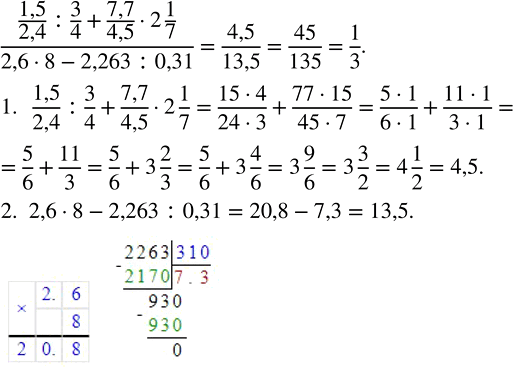
Решение #2 (Учебник 2023)


Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Выполните действия: (1,5/2,4 : 3/4 + 7,7/4,5 · 2 1/7)/(2,6 · 8 - 2,263 : 0,31).
Учитывая то, что черту дроби можно заменить делением, дробное выражение (1,5/2,4 :3/4+7,7/4,5•2 1/7)/(2,6•8-2,263:0,31) преобразуем в выражение
(1,5/2,4 :3/4+7,7/4,5•2 1/7):(2,6•8-2,263:0,31)
Далее в полученном выражении сначала выполняем действия в скобках, затем за скобками.
Причём в каждой скобке сначала выполняем действия второй ступени (умножение и деление) по порядку слева направо, а затем действия первой ступени (сложение и вычитание).
При выполнении вычислений опираемся на следующие правила:
- произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
- для того, чтобы разделить одну дробь на другую, необходимо делимое умножить на число, обратное делителю, то есть у делителя поменять местами числа, стоящие в числителе и знаменателе.
- для того, чтобы разделить десятичную дробь на десятичную, необходимо перенести в делимом и делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе; выполнить деление на натуральное число, то есть разделить дробь на это число, не обращая внимания на запятую; поставить в частном запятую, когда кончится деление целой части. При этом учитываем то, что любое натуральное число можно представить в виде десятичной дроби с каким угодно количеством нулей после запятой.
- для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
- также при вычислениях с обыкновенными дробями, если возможно, выполняем сокращение.
(1,5/2,4 :3/4+7,7/4,5•2 1/7):(2,6•8-2,263:0,31)=(15/24 :3/4+77/45•15/7):(2,6•8-226,3:31)=((3•5)/(3•8)•4/3+77/45•15/7):(2,6•8-226,3:31)=((5•4)/(8•3)+(77•15)/(45•7)):(2,6•8-226,3:31)=((5•4)/(4•2•3)+(7•11•15)/(3•15•7)):(2,6•8-226,3:31)=(5/6+11/3):(2,6•8-226,3:31)=(5/6+3 2/3):(2,6•8-226,3:31)=(5/6+3 (2•2)/(3•2)):(2,6•8-226,3:31)=(5/6+3 4/6):(2,6•8-226,3:31)=3 (5+4)/6:(2,6•8-226,3:31)=3 9/6:(2,6•8-226,3:31)=3 (3•3)/(3•2):(2,6•8-226,3:31)=(3+1 1/2):(20,8-7,3)=4,5:13,5=4,5/13,5=45/135=(45•1)/(45•3)=1/3
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







